Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.2 - Ex. 58

Encontre o volume do sólido S descrito. A base de S é uma região triangular com os vértices ( 0,0 ) , 3,0 e 0,2 . As secções transversais perpendiculares ao eixo y são semicírculos.

Passo 1

Inicialmente, vamos fazer um esboço para entender melhor o que está acontecendo.

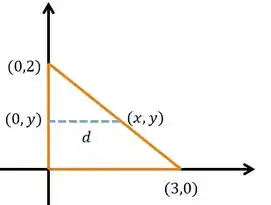
Como as seções transversais são semicírculos, isso quer dizer que a reta pontilhada é o diâmetro da circunferência. Então, vamos achar a equação da reta que liga ( 0,2 ) e ( 3,0 ) para escrever o diâmetro em função de y .

y - 2 = 2 - 0 0 - 3 ⋅ x - 0

Logo,

y - 2 = - 2 3 x     ( i )

Então o diâmetro fica o seguinte:

d = x

Da expressão ( i ) :

d = 3 2 2 - y

Isto é,

d = 3 - 3 2 y

Passo 2

Como queremos rotacionar em torno do eixo y podemos usar o método dos discos integrando de y = 0 até y = 2 , assim:

V = ∫ 0 2 A y d y

Então vamos achar encontrar a área do semicírculo.

A y = π r 2 2

Como já sabemos o diâmetro do Passo 1 vamos colocar em função dele:

A y = π 2 d 2 2

Logo,

A y = π 8 3 - 3 2 y 2

Voltando para nossa integral:

V = ∫ 0 2 π 8 3 - 3 2 y 2 d y

Não esquece: ∫ x n d x   = x n + 1 n + 1 + c   quando   n   ≠ - 1

Passo 3

Tirando o que é constante da integral:

V = π 8 ∫ 0 2 3 - 3 2 y 2 d y

Abrindo esse termo ao quadrado:

V = π 8 ∫ 0 2 9 - 9 y + 9 4 y 2 d y

Agora vamos integrar!

V = π 8 9 y - 9 ⋅ y 2 2 + 9 4 ⋅ y 3 3 0 2

Aplicando entre os pontos 0 e 2 :

V = π 8 9 ⋅ 2 - 9 ⋅ 2 2 2 + 9 4 ⋅ 2 3 3 - 9 ⋅ 0 - 9 ⋅ 0 2 2 + 9 4 ⋅ 0 3 3

Fazendo as contas:

V = 3 4 π

Resposta

V = 3 4 π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

5 - O sólido está situado entre os planos perpendiculares ao eixo x em x = 0 e x =4 . As seções transversais do sólido perpendiculares ao eixo x entre esses planos são discos circulares cujos diâmetro
4 - O sólido está situado entre os planos perpendiculares ao eixo x em x = 0 e x = 6. As seções transversais entre esses planos são quadrados cujas bases vão do eixo x à curva x 1 2 + y 1 2 = 6
6 - A base do sólido é a região limitada pela parábola y 2 = 4 x e pela reta x=1 no plano xy. Cada seção transversal perpendicular ao eixo x é um triângulo equilátero com um lado no plano. (Todos os t
Encontre o volume comum a duas esferas, cada uma com raio r , se o centro de cada esfera estiver na superfície da outra esfera.