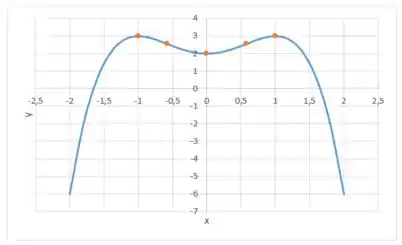
(a) Encontre os intervalos em que a função é crescente ou decrescente.
(b) Encontre os valores máximos ou mínimos locais.
(c) Encontre os intervalos de concavidade e os pontos de inflexão.
(d) Use as informações das partes (a)-(c) para esboçar o gráfico.
Passo 1
Fala aí, tudo belezinha com você?
Bom, essa questão dá pra gente a função
E teremos que dizer algumas coisas sobre ela.
No item (a) precisamos encontrar os intervalos nos quais a função é crescente ou decrescente.
Para saber isso podemos usar as informações dadas pela derivada da função, pois ela representa a inclinação da reta tangente ao gráfico da função. Assim, se
Significa que a função é crescente, já que a reta tangente tem derivada positiva. E se
A função é decrescente, já que a derivada é negativa.
No item (b), queremos encontrar os valores de máximo e mínimo locais.
Para isso também usamos a ideia dada pela inclinação da reta tangente. Ou seja, a derivada. Assim:
Teremos um ponto de máximo ou mínimo da função, já que a inclinação da reta tangente será nula.
No item (c) vamos encontrar os intervalos de concavidade e os pontos de inflexão.
E aqui faremos uso da derivada segunda. Sabendo que se:
Nossa curva terá concavidade para baixo.
E se
E nossa curva terá concavidade para cima.
E finalmente, no item (d) vamos usar as informações das partes (a)-(c) para esboçar o gráfico de .
Agora que já sabemos o que fazer em cada item, vem comigo que te mostro como vai ficar tudo isso.
Passo 2
Pra responder a letra (a) temos que ter em mente que a função é crescente para e decrescente para . Então precisamos derivar :
Usando a regra do expoente, ficamos com:
Vamos dar uma arrumadinha pra facilitar a análise de sinal, colocando o em evidêncida.
E fatorando mais um pouco em diferença de quadrados, teremos
Como estamos interessadado nos valores em que
Vamos descobrir as raízes de cada um dos fatores de e montar a tabela de sinais abaixo.
E ver onde o produto entre os sinais nos dará um resultado positivo.
Estudando o sinal temos a tabela:

Portanto, é decrescente para valores de nos intervalos e e crescente nos intervalos e .
Passo 3
Para encontrar os valores máximos ou mínimos locais precisamos saber os pontos onde a derivada é igual a zero:
Isso acontece em , .
Pegando uma colinha do passo anterior:
Como cresce até e decresce a partir dele, é ponto de máximo local.
Como decresce até e cresce a partir dele, é ponto de mínimo local.
Como cresce até e decresce a partir dele, é ponto de máximo local.
Calculando:
Passo 4
Para encontrarmos os intervalos de concavidade temos que ter em mente que:
A concavidade de uma função é indicada pelo sinal da derivada segunda. Quando a derivada segunda é positiva, a função possui concavidade voltada para cima e quando a derivada segunda é negativa, a função possui concavidade voltada para baixo.
Então devemos obter a derivada segunda e estudar o seu sinal:
Para
Isso significa que:
Para
Assim:
ou
Logo, possui concavidade para cima para valores de no intervalo e concavidade para baixo para valores de no intervalo e . E os pontos de inflexão são e .
Passo 5
Vamos fazer um resumão das nossas informações:
- é decrescente para valores de nos intervalos e e crescente nos intervalos e .
- é ponto de máximo local, é ponto de mínimo local e é ponto de máximo local.
- possui concavidade para cima para valores de no intervalo
- possui concavidade para baixo para valores de no intervalo e
- Pontos de inflexão são e .
Nosso gráfico vai ficar com essa cainha aqui:
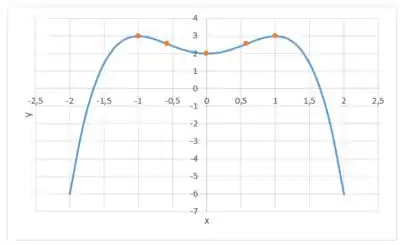
Resposta
(a) é decrescente para valores de nos intervalos e e crescente nos intervalos e .
(b) é ponto de máximo local, é ponto de mínimo local e é ponto de máximo local.
(c) possui concavidade para cima para valores de no intervalo e concavidade para baixo para valores de no intervalo e . E os pontos de inflexão são e .
(d)