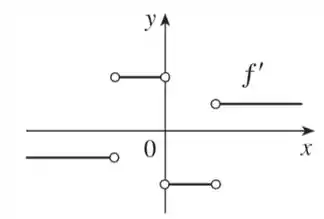
Trace ou copie o gráfico da função dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo para esboçar o gráfico de .
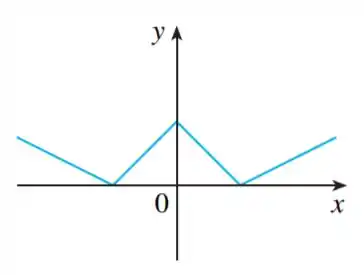
Passo 1
Preparados para mais um exercício sobre gráficos de derivadas? Sim? Então bora meter ficha!
Para esboçar o gráfico da derivada, temos que prestar atenção em alguns pontos do gráfico original. Que é esse aqui:
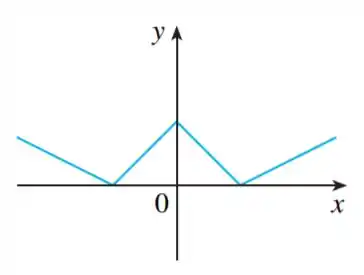
Nos intervalos onde a função decresce, a derivada será negativa. Nos casos em que cresce, será positiva, não se esqueçam!
Bora ver isso com calma. Vem que te ajudo.
Passo 2
Vale ressaltar que, quanto mais rápido ta aumentando ou diminuindo os valores na função, mais longe o eixo estarão os pontos correspondentes no gráfico da derivada, beleza? Isso vai ajudar a dar o formato do desenho.
Além disso, temos que procurar os pontos onde temos uma tangente na horizontal – como a derivada é a inclinação da reta tangente, nesses pontos, a será zero.
Algo EXTREMAMENTE importante – aqui nesse gráfico, vamos ter um ponto onde a derivada não existe! Toda vez que temos uma quina no gráfico de , teremos uma descontinuidade no gráfico de . É essencial que a gente destaque esses pontos, ok?
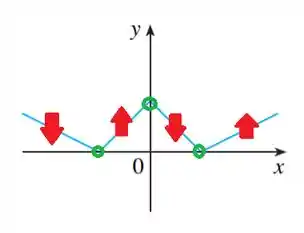
Agora, vamos começar a nossa análise do gráfico. No desenho, as setas em vermelho indicam se o trecho está crescendo ou decrescendo, enquanto o ponto de descontinuidade está circulado em verde. Percebeu?
Passo 3
Agora que os pontos principais de foram destacados, não teremos problemas em desenhar o gráfico de ’! Tudo o que precisamos é seguir as regras ditas no início do passo . Dá uma olhada em como vai ficar a comparação entre o gráfico original e o da sua derivada:
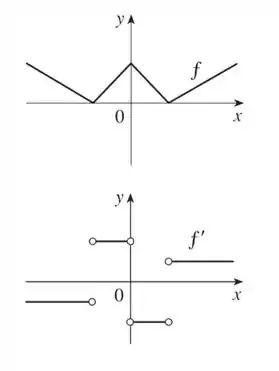
Perceba que o gráfico de Tem três pontos onde é descontinuidade – o mesmo número de pontos onde temos quinas no gráfico de .
Outra coisa para sustentar o nosso esboço: como é feita com um conjunto de retas com uma inclinação diferente de zero, é de se imaginar que o gráfico de tenham várias retas na horizontal. Isso é porque toda função de primeiro grau (uma reta com inclinação diferente de zero) tem como derivada uma constante (representada por uma reta na horizontal), entendido?
Pronto! Já analisamos nosso gráfico de , esboçamos o de e detonamos esse exercício!
Resposta
O esboço de será o seguinte: