Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.8 - Ex. 9
Use o método de Newton com a aproximação inicial para achar , a segunda aproximação da raiz da equação . Faça o gráfico da função e da reta tangente no ponto . Usando este gráfico explique como o método funciona neste caso.
Passo 1
Fala aí! tudo certinho?
Nesse problema foi dada a equação
E nosso objetivo é aplicar o método de Newton para encontrar a partir do chute inicial . Além disso temos que plotar o gráfico da equação e da sua reta tangente no ponto relacionando com o método.
Parece complicado?
Vamos lá aplicar o método de Newton, para isso vamos usar sua fórmula:
O método consiste em aplicar a fórmula repetidas vezes até um determinado valor de ou até uma precisão definida.
Nesse caso, a função é obtida a partir da equação
Bora lá!
Passo 2
Vamos começar montando nossa fórmulinha...
Pra isso precisamos de : pela regra da potencia, temos:
Com isso, nossa fórmulinha fica:
Tranquilo até aqui?
Passo 3
Como queremos vamos usar , e já que já temos que não nos falta nada para substituir, vamos lá então:
Substituindo ...
Vamos achar a reta tangente para poder traçar ela, temos dois pontos e , vamos então jogar os dois pontos na fórmula da reta para achar a inclinação:
Pronto, já temos a equação da reta:
Show?
Passo 4
Vamos agora plotar os gráficos da reta tangente e da função...
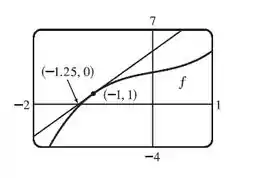
O gráfico mostra a geometria atrás do método de Newton, como , a reta tangente em tem equação igual a , e o zero dessa reta está na aproximação .
E aí! entendeu tudo? Responde Aí!
Resposta
