Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.8 - Ex. 7
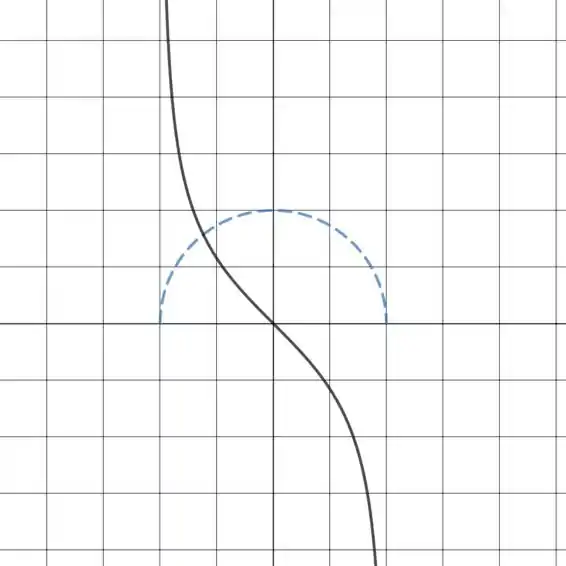
Trace ou copie o gráfico da função dada. (Suponha eixos com a mesma escala.) Use então o método do Exemplo para esboçar o gráfico de .
Passo 1
Fala aí! tudo certinho? 👀
Nesse problema temos o gráfico de uma função e nosso objetivo é obter a partir de .
Vamos utilizar o método do Exemplo 1 para fazermos isso, já que é assim, vamos dar uma olhada neste exemplo.
O Exemplo 1 nos diz que podemos estimar o valor da derivada para qualquer valor de traçando a tangente no ponto e estimando a inclinação. Então se escolhe determinados pontos, cria-se uma reta tangente naquele ponto onde ela é a hipotenusa do triangulo retângulo necessário para calcularmos a inclinação da reta tangente.
Parece difícil? 😉
Passo 2
Usando o gráfico de , podemos fazer as seguintes observações sobre o gráfico de :
Vamos supor que os dois pontos de interseção de com o eixo sejam e , onde é um número positivo.
1) À medida que você se aproxima de , as tangentes se tornam quase verticais (com inclinação muito positiva) até se tornarem verticais em ("inclinação infinita"), então aumenta muito e se aproxima de conforme se aproxima de pela direita.
2) Como há um máximo local em , a tangente em é horizontal, com inclinação , e .
3) Como o gráfico de é contínuo e suave em todos os lugares, o gráfico de é contínuo entre e .
4) diminui de para conforme aumenta de para , já que a taxa de diminuição é muito maior inicialmente e desacelera depois. O gráfico de é côncavo para cima entre e .
5) À medida que você se aproxima de , as tangentes se tornam quase verticais (com inclinação muito negativa) até se tornarem verticais em ("inclinação infinita negativa"), então diminui muito e se aproxima de conforme se aproxima de pela esquerda.
6) diminui de para conforme aumenta de para , já que a taxa de diminuição é mais lenta inicialmente e muito maior conforme se aproxima de . O gráfico de é côncavo para baixo entre e .
7) Como a concavidade muda em enquanto é contínua, este é um ponto de inflexão para .
O gráfico de é mostrado abaixo em cor preta sólida.
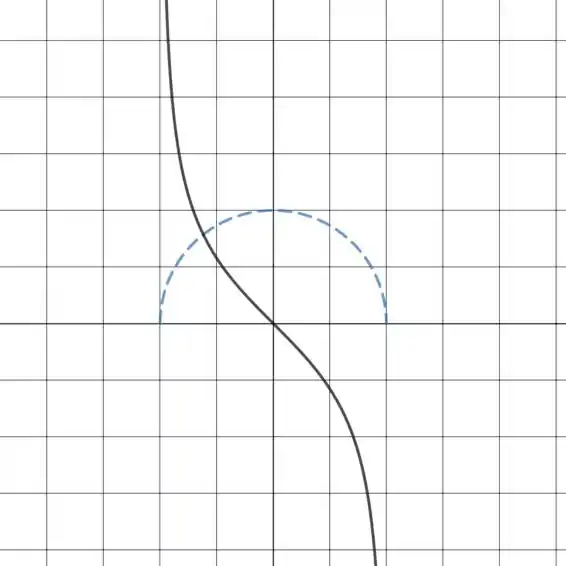
E aí! o que achou? Responde Aí! 👀
Resposta
