Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.6 - Ex. 2
O gráfico de pode interceptar uma assíntota vertical? E uma assíntota Horizontal? Ilustre com gráficos.
Quantas assíntotas horizontais pode ter o gráfico de ? Ilustre com gráficos as possibilidades.
Passo 1
Bora lá! Vamos entender esse problema!!
Antes da gente começar qualquer coisa, o enunciado fala sobre “o gráfico de ” mas que gráfico é esse?!
Aqui a gente vai assumir que é um gráfico qualquer que possua uma assíntota!
Com isso em mente, vamos nessa!!!
Passo 2
Começando pela letra (a) que pergunta se o gráfico de pode interceptar uma assíntota vertical e uma assíntota horizontal e pede pra a gente ilustrar.
Uma assíntota vertical de uma função qualquer, , é uma equação do tipo , sendo uma constante, ou seja, uma reta.
Ela aparece quando a gente tem o limite da função , da seguinte forma:
Nesse caso dizermos que é uma assíntota.
Mas só de observar o limite a gente vê que apenas no inifinito, ou menos infinito! Na prática chega muito perto de interceptar a assíntota, mas nunca chega nela!
Pra ilustrar, vamos fazer :
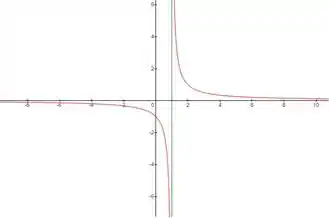
Nesse caso a assíntota é e como a gente pode ver, a função não a intercepta!
Passo 3
Agora, seguindo o mesmo raciocínio, vamos pensar no que é uma assíntota horizontal.
Aí você me fala: Se uma assíntota vertical vai ser uma “reta na vertical” então uma assíntota horizontal é uma “reta na horizontal”, correto?!
Isso aêee!
E ela vai acontecer na seguinte situação:
E o que tá acontecendo aqui?! Quando a gente joga para mais infinito ou menos infinito é igual a , logo a assíntota é .
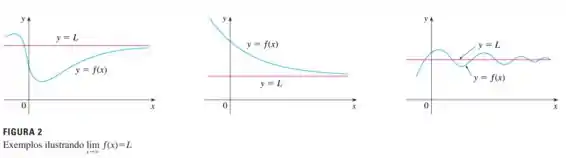
Mas temos um porém: nós podemos, sim, interceptar assíntotas horizontais! Para ilustrar, temos as funções do próprio livro.
Elas são as figuras 2, 3 e 7, por exemplo. Nelas, podemos ver que o gráfico intercepta a assíntota horizontal. Beleza??
Passo 4
Agora a gente quer saber quantas assíntotas um gráfico de uma função pode ter!!
E ela pode ter uma, duas ou nenhuma assíntota! Vamos ver alguns exemplos!
Uma assíntota:
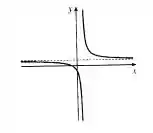
Duas assíntotas:
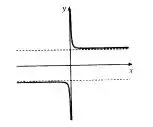
Nenhuma assíntota:
Resposta
- Um gráfico não pode interceptar nem uma assíntota vertical, mas pode interceptar a horizontal.
- pode ter uma, duas ou nenhuma assíntota.