Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.2 - Ex. 64
Trace a curva
Se essa curva girar em torno do eixo , calcule a área da superfície resultante. (Use o gráfico para ajudar a encontrar o intervalo correto do parâmetro.)
Passo 1
Oie, tudo bem? Vamos resolver essa atividade juntos?
Veja bem, a gente tem a curva:
E precisamos encontrar o seu gráfico.
para fazer isso, podemos dar valores para e ver “para onde vai” e .
Após isso, iremos calcular a área de uma superfície de revolução, para isso iremos utilizar a formula:
Então vamos aos cálculos!!
Passo 2
Primeiro vamos plotar o gráfico, eu vou utilizar o GeoGebra, mas você pode fazer na mão, como a gente comentou, você precisa colocar diversos valores para e ir desenhando os pontos.
se temos
e
Se temos
e
Assim, ficamos com o seguinte gráfico:
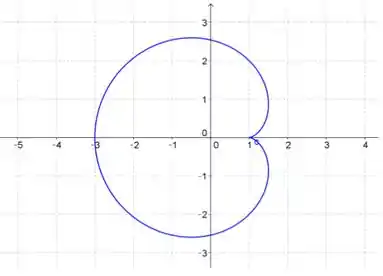
Passo 3
A parte de cima da figura é desenhada no sentido anti-horário de para , como vamos racioná-la ao redor do eixo , basta pegar esse intervalo de então esses são os limites de integração que vamos precisar usar.
Vamos começar encontrando as derivadas parciais:
Vamos então derivar:
E
Substituindo então na formula:
Fazendo esses produtos notáveis e ganhando de brinde uma equação gigante:
Vamos juntar as identidades trigonométricas :
Substituindo então:
Para resolver essa integral vamos lembrar da identidade trigonométrica que diz que: e
Realizando o produto:
Utilizando novamente a identidade trigonométrica :
Temos então:
Colocando a em evidencia:
Retirando as constantes da integral:
Vamos usar mais uma vez que :
Colocando dentro da integral:
Temos então uma integral possível de se calcular:
Vamos realiza rentao uma substituição para realizar essa integral:
Integrando a gente encontra:
Agora é colocar os limites de integração:
E partir para o abraço:
Temos então: