Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 13

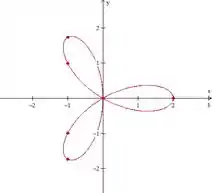
Esboce a curva e calcule a área limitada por ela

r = 2 cos ⁡ 3 θ

Passo 1

Oie, tudo bem com você? Vamos resolver uma atividade juntos hoje.

Dada a curva parametrizada em coordenadas polares:

r = 2 cos ⁡ 3 θ

Precisamos esboçar essa curva, e precisamos calcular a área delimitada por ela. Famílias de curvas com equações:

r = a cos ⁡ n ⋅ θ

r = a sin ⁡ n ⋅ θ

Com n ∈ Z , são chamadas de rosáceas. Temos algumas características nessa família, quando n é par, a rosácea tem 2 n pétalas. Já quando n é ímpar, a rosácea tem n pétalas. O espaçamento entre os eixos das pétalas é dado por 360 º - p , em que p é o número de pétalas.

A área de uma curva em coordenadas polares é dada por:

A = ∫ a b 1 2 r 2 d θ

Então temos que identificar cada termo dessa integral aí, substituir e calcular. Veja que os limites de integração nós encontramos analisando qual o intervalo necessário para que θ consiga varrer toda a figura.

Passo 2

Primeiro vamos esboçar nossa curva, depois a gente calcula a área.

Para esboçar, vamos escolher alguns valores de θ dentro do intervalo 0 ≤ θ ≤ 2 π e obter os valores de r correspondentes. Assim a gente plota os pontos ( r , θ ) , depois liga.

Vamos fazer dessa forma manual porque nessa questão ele não pede para usar ferramenta gráfica, ok?

Plotando esses pontos e ligando tudo, vamos ter a curva:

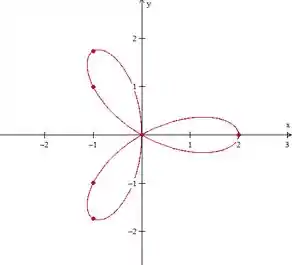
Agora sim vamos calcular a área da curva!

Passo 3

O intervalo de integração seria o intervalo em que a curva está definida:

a = 0

b = 2 π

Maaaas, repare que a curva é simétrica e pode ser dividida em 6 partes iguais, se a gente dividir cada “pétala” pela metade.

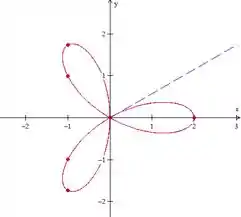
Olhando somente para a pétala que tá no lado direito da figura, a metade dela está limitada pelo eixo polar θ = 0 e θ = π 6 . Assim, podemos fazer:

0 ≤ θ ≤ π 6

E calcular a área da curva apenas nesse intervalo e depois multiplicar por 6. Beleza?

Continuando, o r é a própria parametrização:

r = 2 cos ⁡ 3 θ

Então é só substituir e integrar esse negócio.

Passo 4

Vamos lá:

A = ∫ a b 1 2 r 2 d θ

r = 2 cos ⁡ 3 θ

Agora vamos iniciar a integral:

A 1 = 1 2 ∫ 0 π 6 2 cos ⁡ 3 θ 2 d θ

Elevando ao quadrado:

A 1 = 1 2 ∫ 0 π 6 ( 4 cos 2 ⁡ 3 θ ) d θ

Retirando a constante da integral:

A 1 = 4 2 ∫ 0 π 6 cos 2 ⁡ 3 θ d θ

Utilizando da identidade trigonométrica cos 2 ⁡ θ = 1 - cos ⁡ 2 θ 2 :

A 1 = 2 ∫ 0 π 6 1 2 ( 1 + cos ⁡ 2 ⋅ 3 θ ) d θ

A 1 = ∫ 0 π 6 ( 1 + cos ⁡ 6 θ ) d θ

Podemos integrar rapidamente pois temos integrais tabelas aqui:

A 1 = θ + 1 6 sen ⁡ 6 θ π 6 0

Colocando os intervalos de integração:

A 1 = π 6 + 1 6 sen ⁡ π - 0 + 1 6 sen ⁡ 0

A 1 = [ π 6 + 0 - 0 + 0 ]

A 1 = π 6

Assim,

A T = A 1 × 6 = π

Resposta

A = π

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da regiao sombreada, onde r = s e n (2 theta) .
Encontre a área da região dentro de um laço, onde r = 4 s e n 3 θ .
Encontre a área da regiao sombreada, onde r = 1 + s e n ( θ ) .
Encontre a área da regiao sombreada, onde r = 4 + 3 s e n ( θ ) .
Seja R a região dentro do laço da curva no Exemplo 1:Calcule a área de R Se R girar em torno do eixo x , encontre o volume do sólido resultante Encontre o centroide de R