Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 13.2 - Ex. 8
(a) Esboce o gráfico da curva plana com a equação vetorial dada.
(b) Determine .
(c) Desenhe o vetor de posição e o vetor tangente para o valor dado de t.
Passo 1
Hey, brother! Vamos resolver juntos essa atividade, confia que você vai aprender tudo hoje!
A gente tem a equação:
E devemos: Esboçar o gráfico dela, determinar a sua derivada e por último devemos esboçar o vetor posição no ponto:
E também o vetor tangente nesse mesmo ponto.
Para esboçarmos o gráfico da equação vetorial podemos montar uma tabela para nos ajudar.
Já o cálculo de temos que derivar cada coordenada da equação vetorial . Em relação ao desenho do vetor, iremos colocar o valor de nas equações e e teremos então as coordenadas de e , começaremos a desenhar o nosso vetor a partir do ponto para o vetor tangente e para o vetor posição nós começamos o seu desenho a partir da origem.
Passo 2
a) Montando a tabela para plotarmos o gráfico:
O gráfico é construído com os valores de e seus respecitivos valores das coordenadas e , juntando os pontos, podemos notar que a nossa figura é:
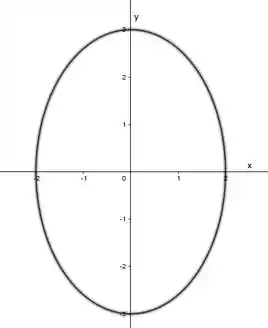
Passo 3
b) A derivada de é:
Derivada da componente :
Derivada da componente :
Desta forma é:
Passo 4
c) O vetor posição é um vetor que parte da origem e no nosso caso queremos que ele vá até o parâmetro .
O vetor tangente é um vetor dado pela derivada da equação vetorial, e queremos o vetor tangente ao parâmetro .
O ponto que corresponde a , é
E para a o nosso vetor tangente, temos:
Desta forma os vetores são:
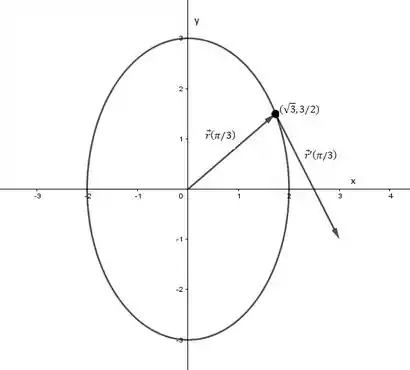
Veja aqui que temos para o vetor posição,
unidades no eixo e unidades no eixo , esse vetor é então desenhado da origem até o ponto .
Para o vetor tangente:
O comportamento é semelhante, porém agora começamos a desenhar o vetor no ponto .
Resposta
b)