Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 10.Revisão - Ex. 57

Uma curva chamada fólio de Descartes é definida pelas equações paramétricas

x = 3 t 1 + t 3       y = 3 t 2 1 + t 3

  1. Mostre que, se ( a , b ) estiverem na curva, então ( b , a ) também está; insto é, a curva é simétrica em relação à reta y = x . Onde a curva intercepta essa reta?
  2. Encontre os pontos na curva onde as retas tangentes são horizontais ou verticais.
  3. Mostre que a reta y   =   - x - 1 é uma assíntota oblíqua.
  4. Esboce a curva.
  5. Mostre que a equação cartesiana dessa curva é x 3   + y 3   =   3 x y .
  6. Mostre que a equação polar pode ser escrita na forma

    7. r = 3 sec ⁡ θ tan ⁡ θ 1 + tan 3 ⁡ θ

  7. Encontre a área da região dentro do laço dessa curva.
  8. Mostre que a área do laço é a mesma que está entre a assíntota e os ramos infinitos da curva. (Use um sistema de computação algébrica para calcular a integral)

Passo 1

Primeira coisa a se fazer ao olhar para esse exercício é chorar. OMG, quanta coisa!!!

Pronto, enxuga as lagrimas, levanta a cabeça e vamos lá!!!

Bom... na verdade as curvas paramétricas do fólio são essas (está incorreto no livro):

x = 3 t 1 + t 3

y = 3 t 2 1 + t 3

Primeiramente, na letra (a) queremos mostrar que a curva é simétrica em relação à reta y = x e mostrar onde a curva intercepta essa reta.

Para isso, temos que provar que o parâmetro t deve ser igual a 1 t .

Em seguida, na letra (b), devemos encontrar os pontos na curva onde as retas tangentes são horizontais ou verticais.

Para isso, podemos escolher uma derivada d y d t uma derivada e igualar a zero para encontrar a reta tangente horizontal. Com a simetria, podemos encontrar o ponto da reta tangente vertical.

Depois, na letra (c), queremos mostrar que a reta y   =   - x - 1 é uma assíntota oblíqua. Para isso, devemos analisar para onde x e y tendem ao infinito.

Na letra (d) queremos esboçar a curva.

Na letra (e) queremos mostrar que a equação cartesiana dessa curva é x 3   + y 3   =   3 x y . Para isso, basta substituirmos as equações paramétricas em x 3   + y 3 para encontrarmos 3 x y .

Na letra (f) queremos mostrar que a equação polar pode ser escrita na forma:

r = 3 sec ⁡ θ tan ⁡ θ 1 + tan 3 ⁡ θ

Na letra (g) queremos a área da região dentro do laço dessa curva. Para isso, basta fazermos a integral dupla (em relação a r e θ ) dessa equação polar acima.

Na letra (h) queremos mostrar que a área do laço é a mesma que está entre a assíntota e os ramos infinitos da curva.

Agora bora lá!! 😉

Passo 2

  1. Primeiro vamos tomar t = 0 , mostrando que o ponto ( 0,0 ) está em nossa curva, ou seja, ela passa pela origem.

    2. Agora vamos fazer a seguinte analise. Se essa curva passa pelo ponto ( a , b ) , ela passa para um dado t = t 1 , ou seja

    a = 3 t 1 1 + t 1 3

    E

    b = 3 t 1 2 1 + t 1 3

    enquanto deve existir um t = t 2 , tal que

    b = 3 t 2 1 + t 2 3

    E

    a = 3 t 2 2 1 + t 2 3

    Concordamos que em ambos os casos, teremos que

    b a = t 1 = 1 t 2

    Isso sugere que, se fizemos uma transformação de t → 1 / t , podemos inverter os ponto de a , b → b , a ? Vamos ver

    x = 3 t 1 + t 3

    = 3 1 t 1 + 1 t 3

    = 3 t 3 t 1 + t 3

    = 3 t 2 1 + t 3 = y

    Isso implica que a curva é simétrica em y = x e que todos os ponto a , b contidos nesta curva possuem seu simétrico b , a .

    Passo 3

  2. Estamos interessados aqui nos pontos que possuem retas tangentes horizontais.

    3. Olhando para o gráfico abaixo, podemos ter uma noção visual de onde estão esses pontos, entretanto iremos usar a técnica de acha-los pelo método algébrico e não geométrico apenas.

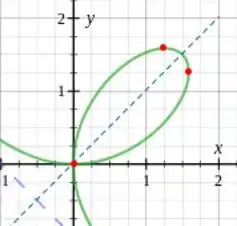
    Para isso vamos simplesmente calcular a derivada de d y d t e igualá-la a zero.

    d y d t = 1 + t 3 6 t - 3 t 2 3 t 2 1 + t 3 2

    6 t - 3 t 4 1 + t 3 2 = 0

    6 t - 3 t 4 = 0

    Assim determinamos os pontos que que t = 0 e t = 2 3 , nos dando os pontos 0,0 e 2 3 , 4 3 .

    Como mostrado no item anterior a simetria de nossa curva, podemos então concluir que os pontos que possuem retas tangentes verticais serão 0,0 e 4 3 , 2 3 .

    Para conferir esse resultado, basta fazer a derivada de x em função de t e igualar a zero.

    Passo 4

  3. Primeira observação que devemos fazer é: observe que quando t → - 1 + , temos que x → - ∞ e y → ∞ . Temos também que, quando t → - 1 - , temos x → ∞ e y → - ∞ .

    4. Agora vamos analisar nossa função y + x + 1 = 0

    y + x + 1 = 3 t + 3 t 2 + 1 + t 3 1 + t 3

    = 1 + t 3 1 + t 3

    = 1 + t 2 1 + t 1 + t 3

    = 1 + t 2 t 2 - t + 1

    Onde

    1 + t 2 t 2 - t + 1 → 0   i m p l i c a   t → - 1

    Logo a equação y = - x - 1 é uma assíntota oblíqua.

    Passo 5

  4. Lembrando de nossas aulas de cálculo 1, devemos lembrar que, para esboçar uma curva, devemos calcular suas derivadas primeiras e segundas e analisá-las com cuidado.

    5. Vamos primeiro calcular d y / d x

    d y d x = d y d t d x d t = t 2 - t 3 1 - 2 t 3

    e

    d 2 y d x 2 = d d t d y d x d x / d t = 2 1 + t 3 4 3 1 - 2 t 3 3

    Os pontos de mínimos e máximos são dados quando a derivada primeira vale zero, logo temos os pontos 0,0 e 2 3 , 4 3 que já aviamos calculados anteriormente.

    Outra coisa é entender suas concavidades, que entre x ∈ - ∞ , 4 3 possui sua concavidade para cima e quando x ∈ 4 3 , + ∞ tem sua concavidade para baixo. Basta tomarmos quando a segunda derivada é positiva e quando ela é negativa respectivamente.

    Passo 6

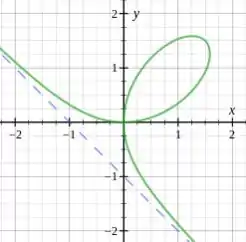
  5. Neste item vamos partir de uma suposição e tentar chegar em uma verdade.

    6. Tome a equação sugerida x 3 + y 3 = 3 x y , então fazemos

    x 3 + y 3 = 3 t 1 + t 3 3 + 3 t 2 1 + t 3 3

    = 27 t 3 + t 6 1 + t 3 3

    = 27 t 3 1 + t 3 1 + t 3 3

    = 27 t 3 1 + t 3 2

    Podemos reescrever da seguinte forma:

    = 3 3 t 1 + t 3 3 t 2 1 + t 3

    Substituindo as equações paramétricas:

    = 3 x y

    Desta forma mostramos que a equação cartesiana desta curva é x 3 + y 3 = 3 x y

    Passo 7

  6. Vamos tomar a equação cartesiana acima e fazer a seguinte substituição x = r cos ⁡ θ e y = r   s e n   θ .

    7. Assim teremos:

    x 3 + y 3 = 3 x y

    r 3 cos 3 ⁡ θ + r 3   s e n 3 θ

    3 r 2 cos ⁡ θ   s e n   θ

    Para r ≠ 0 teremos

    r = 3 cos ⁡ θ s e n   θ cos 3 ⁡ θ + s e n 3 θ

    = 1 cos 3 ⁡ θ ⋅ 3 cos ⁡ θ s e n   θ 1 + s e n 3 θ cos 3 ⁡ θ

    = 3 1 cos ⁡ θ s e n   θ cos ⁡ θ 1 + s e n 3 θ cos 3 ⁡ θ

    = 3 sec ⁡ θ tan ⁡ θ 1 + tan 3 ⁡ θ    

    Uma manipulação matemática as vezes meio chata, mas aí está!! 😉

    Passo 8

  7. O laço do fólio de Descarte se encontra presente apenas no primeiro quadrante, desta forma temos que θ ∈ [ 0 , π / 2 ] .

    8. Assim teremos

    A = ∬ d A

    A = ∫ 0 π 2 ∫ 0 r r   d r   d θ

    A = ∫ 0 π 2 r 2 2   d θ

    A = 9 2 ∫ 0 π 2 sec ⁡ θ tan ⁡ θ 1 + tan 3 ⁡ θ 2   d θ

    Vamos tomar u = tan ⁡ θ assim conseguimos resumir nossa integral em

    A = 9 2 ∫ 0 ∞ u 2 d u 1 + u 3 2

    A = lim b = ∞ ⁡ 9 2 - 1 3 1 + u 3 - 1 0 b

    A = 3 2

    Passo 9

  8. E finalmente a última alternativa, que óbvio não seria algo simples hahaha.

Vamos olhar para a área que delimitada pela curva e pela assíntota.

Reparamos que o que a compões são o segundo, terceiro e quarto quadrante, na qual a área do segundo e do quarto são iguais.

Observe também que a área do terceiro quadrante é ½ .

Fica agora apenas para a gente calcular a área do segundo quadrante.

Tome a equação da assíntota y = - x - 1 e vamos tomar a parametrização utilizada no passo 7.

Com isso temos

r   s e n   θ = - r cos ⁡ θ - 1

r =   - 1 s e n   θ + cos ⁡ θ

Desta forma basta fazermos

A 2 = ∫ r 2 2   d θ

A 2 = 1 2 ∫ 3 π 4 π - 1 s e n   θ + cos ⁡ θ 2 + 3 sec ⁡ θ tan ⁡ θ 1 + tan 3 �� θ 2 d θ  

Aqui usamos um sistema de computação algébrica, chegando em

A 2 = 1 2

Assim teremos que a área total é dado por

A T = 2 A 2 + A 3

A T = 2 1 2 + 1 2

A T = 3 2

Que é exatamente a área do laço.

Ps: O autor dessa resolução quase morreu durante seu trabalho haha

Resposta

(a) Demonstração

(b) retas tangentes verticais serão 0,0 e 4 3 , 2 3 .

(c) Demonstração

(d)

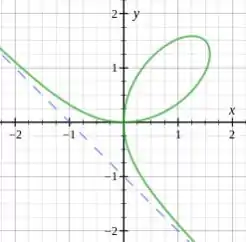
(e)Demonstração

(f) Demonstração

(g) A = 3 2

(h) Demonstração

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a área da região delimitada pela hipérbole x 2 a 2 - y 2 b 2 = 1 e pela reta vertical passando por um foco.
(a) Se uma elipse é girada em torno de seu eixo maior, encontre o volume do sólido resultante.(b) Se ela for girada em torno de seu eixo menor, encontre o volume resultante.
Calcule a área da região limitada pelo astroide x = a * cos 3 ⁡ θ ,y = a * s e n 3 θ (Os astroides foram explorados no Projeto de Laboratório na página 597).
Encontre a área sobre um arco de trocoide do Exercício 40, na seção 10.1, para o caso de dr .
Use as equações paramétricas de uma elipse x = a cos ⁡ θ y = b sen ⁡ θ 0 ≤ θ ≤ 2 π Para calcular a área limitada por essas curvas.