Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.4 - Ex. 50
Use uma calculadora ou um computador para encontrar o comprimento do laço, com precisão de quatro casas decimais.
Passo 1
Falaeee, beleza?? Bom... o enunciado nos deu a seguinte expressão de uma curva (dada em coordenadas polares):
Queremos calcular o comprimento de um laço dessa curva com precisão de casas decimais.
E, para isso, o enunciado nos pede para usarmos uma calculadora ou um software matemático.
Espera um pouco... Como assim laço??
Bom... se a gente plotar nossa curva, obteremos a seguinte figura:
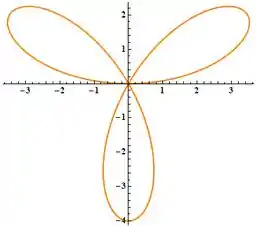
Perceba que parece uma flor com três pétalas. Assim, queremos calcular o comprimento de uma dessas “pétalas”.
Para isso, o comprimento é dado por:
Agora podemos aplicar!!! 😉
Passo 2
Vamos calcular primeiro a derivada de .
Sabemos que:
Derivando, temos:
Colocando a constante para fora:
E aplicando a Regra da Cadeia:
Passo 3
Desta forma, como e geramos essa figura para :
Resolvendo com o auxílio de uma calculadora, teremos: