Traçe o esbolço do gráfico de uma função f no intervalo I em cada caso: (a) I é um intervalo aberto (0,2) e f é contínua em I. Em 1, f tem um valor máximo relativo, mas não existe. (b) I é o intervalo fechado [0,2]. A função f tem um valor mínimo relativo em 1, mas o valor mínimo absoluto de f está em 0. (c) I é o intervalo aberto (0,2), e tem um valor máximo relativo em 1.
Passo 1
Sabendo que, um caso na a função é contínua no ponto, mas não existe derivada no mesmo é na função modular. Desse modo, tanto no item (a) quanto no item (b) a função é modular, no mais vai mudar os coeficientes.
Passo 2
Primeiro vamos pensar em uma função contínua em 1 mas não existe derivada neste ponto. Esta função pode ser . Note que, ela é contínua, mas não existe derivada.
Porém o item pede que em 1 tenha um valo máximo, ou seja a concavidade é voltada para baixo, desse modo basta mudarmos a concavidade para baixo da nossa função. Com isso,
O esbolço do gráfico é dado:
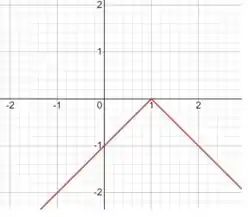
Passo 3
Para o item (b) vamos continuar utilizando a função modular, porém pode utilizar outras funções, pois a questão não especifica. Desse modo, vamos pensar em um função que tem mínimo relativo em 1 e absoluto em 0.
Podemos escolher esta função,
Percebe-se que, os valores foram bem escolhidos para atender o que a questão pede, dessa maneira, note que existe um mínimo relativo em 1 pois a função está decrescendo e depois do ponto ela cresce e no 0 têm o mínimo absoluto.
Assim, o gráfico é:
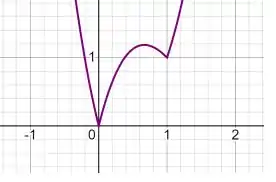
Passo 4
Para o item (c) temos o máximo relativo em 1, apenas, ou seja, uma função simple que tem o máximo relativo em 1 é a primeira que escolhemos
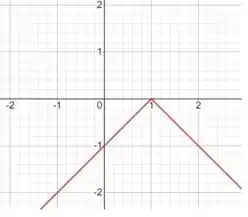
Resposta
Ei, a resposta está no passo a passo :)