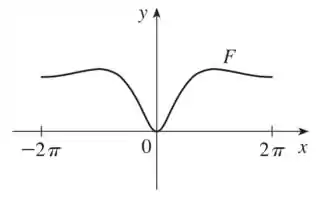
Trace um gráfico de e use-o para fazer um esboço da primitiva que passe pela origem.
Passo 1
Fala aí, belezinha?
Bom, nessa questão estamos interessados em traçar um gráfico para a primitiva da função
Para isso, iremos utilizar os conceitos de derivada de decrescimento, crescimento, valores de máximo, valores de mínimo e pontos de inflexão para esboçar uma primitiva de .
E teremos que lembrar que quando:

Olhando para o gráfico dado, podemos analisar o que está acontecendo com a primitiva da nossa função com base, nas informaç��es sobre sua derivada.
Vem que te mostro como.
E aí? Bora lá?? 😉
Passo 2
Então... para esboçar graficamente vamos pensar um pouco... se liga da função:
Perceba que o numerador é uma função seno (que tem valor máximo ) e que, quanto mais aumentamos o valor de , o denominador se torna maior que o numerador.
Mas o que significa isso?? Significa que próximo da origem o gráfico apresentará uma oscilação e que esse irá se aproximando de zero quanto mais a gente se afasta da origem.
Com isso, temos o seguinte gráfico:
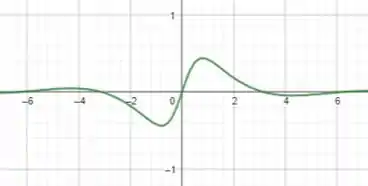
A partir desse gráfico, podemos extrair algumas informações para gerarmos o gráfico da nossa primitiva .
Passo 3
Após esboçar o gráfico, poderemos ver que nos pontos de máximo e mínimo deverá haver um ponto de inflexão no gráfico de . Já que:

Além disso, nos valores em que é negativa, deverá estar decrescendo e nos valores que é positiva, deverá crescer. Já que

Também, nos valores onde sai do positivo para o negativo, deveremos ter um ponto de máximo e nos valores aonde sai do negativo para o positivo, deveremos ter um ponto de mínimo.
Com base no gráfico de , podemos esboçar o gráfico de :
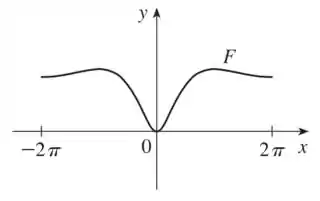
Entendeu direitinho?? Responde aee 😉
Resposta