Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.9 - Ex. 59

Uma partícula move-se de acordo com os dados a seguir. Encontre a posição da partícula.

v t = s e n   t - cos ⁡ t ,             s 0 = 0

Passo 1

Eaeeee, belezinha?? Bom galera... nessa questão queremos encontrar a posição da partícula que se move de acordo com a seguinte função velocidade dada:

v t = s e n   t - cos ⁡ t

Dado que s 0 = 0 .

Para isso, deveremos encontrar a função posição s ( t ) da partícula, que é a antiderivada de v ( t ) .

E aí? Bora lá??

Passo 2

Para encontrar a primitiva de v ( t ) iremos utilizar as regras de derivação de funções trigonométricas.

Também podemos utilizar a tabelinha mostrada na seção 4.9 que mostra a função e sua primitiva particular:

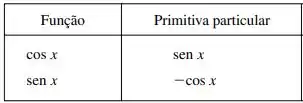
Assim, temos:

v t = s e n   t - cos ⁡ t ∴

s t = - cos ⁡ t - s e n   t + C

Derivando s ( t ) , temos:

s ' t = s e n   t - cos ⁡ t = v ( t )

Dessa forma, podemos concluir que s ( t ) é a antiderivada de v ( t ) .

Passo 3

Iremos agora encontrar o valor da constante C utilizando a condição dada.

Aplicando s 0 = 0 , temos:

s t = - cos ⁡ t - s e n   t + C ∴

s 0 = - cos ⁡ 0 - s e n   0 + C ∴

0 = - cos ⁡ 0 - s e n   0 + C ∴

C = 1

Logo, temos que a posição da nossa partícula é dada pela seguinte equação:

s t = - cos ⁡ t - s e n   t + 1

Entendeu direitinho?? Responde aee 😉

Resposta

s t = - cos ⁡ t - s e n   t + 1

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um modelo de foguete é lançado para cima a partir do repouso. Sua aceleração para os três primeiros segundos é a t = 18 t , e nesse ínterim o combustível acaba, e ele se transforma em um corpo em qued
Encontre a primitiva F de f que satisfaça a condição dada. Verifique sua resposta comparando os gráficos de f e F f x = 5 x 4 - 2 x 5 , F 0 = 4
Encontre f . f ' x = 1 - 6 x , f 0 = 8
Encontre f . f ' x = 8 x 3 + 12 x + 3 , f 1 = 6
Encontre a primitiva F de f que satisfaça a condição dada. Verifique sua resposta comparando os gráficos de f e F f x = 4 - 3 1 + x 2 - 1 ,F 1 = 0