Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.2 - Ex. 17

  1. Trace-as raízes de cada polinômio em uma reta, juntamente com os zeros de sua primeira derivada.

    2. i )   y = x 2 - 4

    i i )   y = x 2 + 8 x + 15

    i i i ) y = x 3 - 3 x 2 + 4 = ( x + 1 ) ( x - 2 ) ²

    i v ) y = x 3 - 33 x 2 + 216 x = x ( x - 9 ) ( x - 24 )

  2. Use o teorema de Rolle para provar que entre duas raízes quaisquer de

x n + a n - 1 x n - 1 + … + a 1 x + a 0

existe uma raiz de

n x n - 1 + n - 1 a n - 1 x n - 2 + … + a 1

Passo 1

Solucionando o item a:

Encontrando as raízes de cada função, teremos:

i )   x 2 - 4 = 0

x 2 = 4

x = 4

x 1 = + 2 ,     x 2 = - 2

i i )   x 2 + 8 x + 15 = 0

Δ = 8 2 - 4 × 1 × 15 = 4

- 8 ± 4 2 × 1 = - 8 ± 2 2

x 1 = - 3 ,     x 2 = - 5

i i i )   x + 1 x - 2 2 = 0

x + 1 x - 2 x - 2 = 0

x 1 = - 1 ,     x 2 = 2 ,     x 3 = 2

i v )   x x - 9 x - 24 = 0

x 1 = 0 ,     x 2 = 9 ,     x 3 = 24

Passo 2

Derivando item a item e igualando a 0, teremos:

i ) y ' = 2 x

2 x = 0

x = 0

i i ) y ' = 2 x + 8

x = - 8 2

x = - 4

i i i )   y ' = 3 x 2 - 6 x

3 x 2 - 6 x = 0

3 x x - 2 = 0

x 1 = 0 ,     x 2 = 2

i v )   y ' = 3 x 2 - 66 x + 216

3 x 2 - 66 x + 216 = 0

Δ = - 66 2 - 4 × 3 × 216 = 4356 - 2592 = 1764

- - 66 ± 1764 2 × 3 = 66 ± 42 6

x 1 = 18 ,     x 2 = 4

Passo 3

Traçando a reta com os pontos da função e o zero da derivada, teremos:

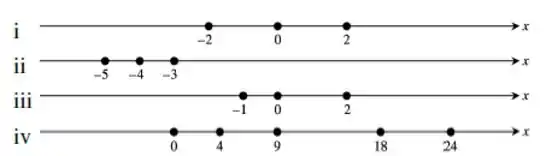
Passo 4

Solucionando o item b:

Sendo:

P x = x n + a n - 1 x n - 1 + … + a 1 x + a 0

P ' x = n x n - 1 + n - 1 a n - 1 x n - 2 + … + a 1

Com base em tudo o que já foi desenvolvido acima, sejam duas raízes a   e b de um polinômio P ( x ) qualquer, temos que P a = P b = 0 . Uma vez que as funções são contínuas e diferenciáveis em todos os pontos do intervalo, o Teorema do valor Médio é aplicável. Logo, temos um valor c , situado entre a   e   b , que satisfaz a expressão P ' c = 0 .

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Mostre que e x 1 x 2 =e x 1 . x 2 = e x 2 x 1 para quaisquer números x1 e x2
Suponha que 0 f' ( x )1 / 2 para todos os valores de x. Mostre que f ( -1 )f ( 1 )2+f ( -1 )
Demonstre que | c o sx-1 | | x | para todos os valores de x. (Dica: considere f t =c o ste m[ 0 ,x ] .)
Use o argumento da mesma derivada para provas as identidades t g - 1 x + c o t g - 1 x = π 2 sec - 1 ⁡ x + c o s s e c - 1 x = π 2