Usando retângulos cujas alturas sejam dadas pelo valor da função no ponto médio da base do retângulo (regra do ponto médio), estime a área sob as curvas das seguintes funções, utilizando primeiro, dois e depois quatro, retângulos.
6. entre e
Passo 1
O gráfico da função é:
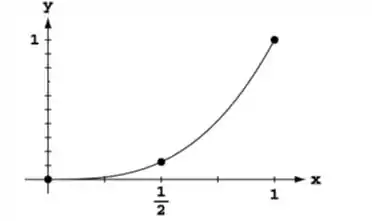
Utilizando dois retângulos de base 1/:
Vamos calcular a altura que é igual ao valor da função no ponto médio do retângulo:
Primeiro:
Segundo:
Calculando a área:
Passo 2
Quatro retângulos de base , vamos calcular suas alturas:
O primeiro:
O segundo:
O terceiro:
O quarto:
Agora fazendo o cálculo da área vamos obter:
Resposta
2 retângulos:
4 retângulos: