Use as assíntotas de para esboçar o gráfico sem recorrer ao procedimento desta seção.
Passo 1
Bom pessoal, o exercício pede para usarmos as assíntotas como guia e não usar o procedimento desta seção. Vamos à função:
A função seno é periódica e está sempre compreendida no intervalo [1,1]. Portanto, não existe limite e não iremos analisar esta função. Vamos analisar a função exponencial:
Logo .
Agora vamos verificar nos infinitos.
Portanto, quando , a função vai tender ao infinito.
Portanto, quando , a função vai tender zero. Porém, isto ocorre de forma gradual. Vamos usar como exemplo:
Podemos então ir traçando o gráfico e vendo a tendência. Conforme o valor de x aumenta, temos que a função se aproxima de Quando a função tende a valores negativos, a função tende a .
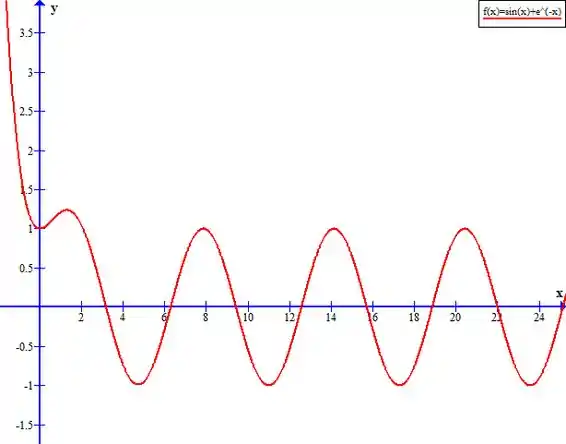
Resposta
Ei, a resposta está no passo a passo :)