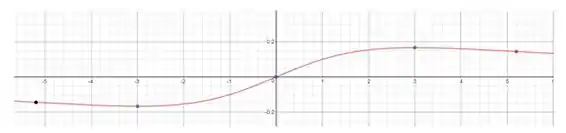
Use o roteiro dessa seção para esboçar a curva.
Passo 1
Oi meus queridos, tudo bem?
Nós temos a função
E aqui vamos seguir o seguinte roteiro para esboçar o gráfico dela.
A. Encontrar o domínio em que a função é definida.
B. Encontrar os interceptos. Que são os pontos onde a função cruza o eixo , isso é:
E o pontos onde a função cruza o eixo , isso é:
C. Verificar se há simetria par, isso é:
Para isso, basta substituir por e verificar se a expressão se mantém a mesma.
E se há simetria ímpar, isso é:
Para isso, basta substituir por e verificar se a expressão vira .
D. Procurar por assíntotas horizontais e verticais.
Uma assíntota horizontal é um valor real para o qual a função tende quando tende para infinito:
Já uma assíntota vertical é um valor de no qual a função possui uma descontinuidade e tende para infinito.
E. Encontrar os intervalos de crescimento e decrescimento. Para isso, basta derivar a função e nos intervalos em que a derivada for positiva a função cresce
E nos intervalos em que a derivada for negativa a função decresce
F. Encontrar os pontos de máximo e mínimo local.
Esses pontos ocorrem quando a derivada vale zero e troca de sinal ou quando a derivada possui uma descontinuidade e troca de sinal.
Caso a derivada fosse negativa e depois do ponto ela é positiva, então a função possui um ponto de mínimo local. Se a derivada era positiva e depois do ponto ela é negativa, então a função possui um ponto de máximo local.
G. Encontrar os intervalos de concavidade e pontos de inflexão.
A concavidade é para cima se a derivada segunda for positiva
E a concavidade é para baixo se a derivada segunda for negativa
Por fim, um ponto de inflexão é um ponto onde a derivada segunda vale zero e troca de sinal.
H. Esboçar a função juntando as informações obtidas.
Passo 2
Como o denominador não pode se anular, devemos ter .
Todavia, como , uma vez que .
Portanto, o domínio será todos os valores reais.
Passo 3
Fazendo , temos:
E fazendo , temos?
Dessa forma, a função cruza o eixo em e cruza o eixo em , portanto, a função passa pela origem .
Passo 4
Observe que a função é ímpar:
Como ela é ímpar, ela apresenta simetria com relação à origem.
Passo 5
Para as assíntotas horizontais, tomamos os limites no infinito:
Podemos resolver a indeterminação por L’hospital.
E para , temos
Resolvendo por L’hospital.
Assim, tanto para como para , a reta é assíntota horizontal da função.
Como o domínio da função é a reta real toda, o gráfico da função não vai apresentar assíntotas verticais.
Passo 6
Para os intervalos de crescimento e decrescimento, precisamos de . Nossa função é:
Portanto, sua derivada será dada por uma regra do quociente.
Como o denominador �� sempre positivo
O termo que vai mandar no sinal de .
Fazendo um estudo de sinais temos:
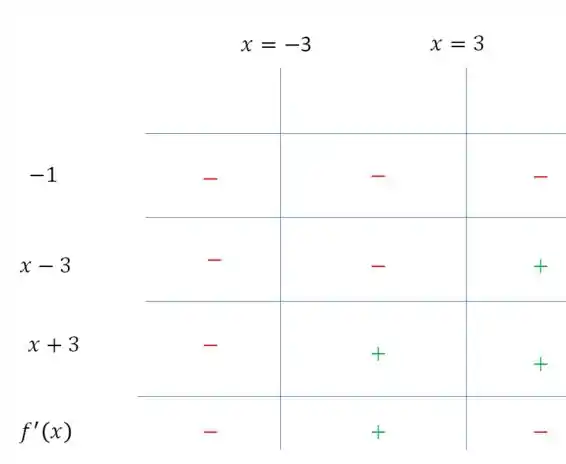
Quando , temos que . Quando , temos que e quando , temos que .
Portanto, nossos intervalos de crescimento e decrescimento são.

Passo 7
Para avaliar os pontos de máximo e mínimo, vamos olhar para os pontos onde a derivada troca de sinal.
Em , a derivada antes era negativa e depois é positiva, portanto, esse é um ponto de mínimo local.
Assim, é ponto de mínimo local
Em , a derivada antes era positiva e depois é negativa, portanto, esse é um ponto de máximo local.
Enquanto que é ponto de máximo local.
Passo 8
Por fim, vamos analisar a concavidade da curva.
A nossa primeira derivada é:
Portanto, derivando a derivada para obter a segunda derivada, temos:
Podemos simplificar um fator , resultando em:
Colocando o em evidência, temos:
Temos que o denominador é sempre positivo
Portanto, quem vai mandar no sinal de serão os fatores do denominador.
E para o outro termo temos:
Tirando a raíz e multiplicando por (lembra que pra multiplicar por , tem que inverter o sinal da desigualdade), temos:
Dessa forma, temos o seguinte estudo de sinais

Portanto, temos que quando e e temos que quando e .
Sendo assim temos a seguinte tabela.

, e são pontos de inflexão.
Jogando esses valores na função original, obtemos as coordenadas dos pontos de inflexão.
Assim, os pontos de inflexão são , e .
Passo 9
O esboço da curva é:
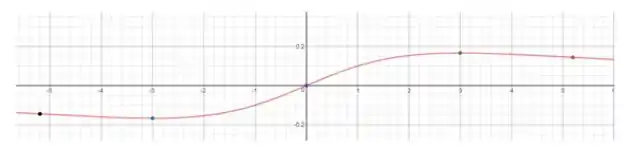
Os pontos demarcados na figura são em ordem: ponto de inflexão, ponto de mínimo, ponto de inflexão, ponto de máximo, ponto de inflexão.
Resposta
O esboço da curva: