Use uma calculadora ou um computador para fazer uma tabela dos valores das somas de Riemann à direita para a integral com , , e . De qual valor esses números parecem estar se aproximando?
Passo 1
Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui iremos utilizar uma calculadora ou seu próprio computador para calcularmos os valores da soma de Riemann á direita da integral dada. O fato de ser a direita, significa que ao criarmos nossos retângulos abaixo do gráfico, iremos utilizar o ponto do lado direito do lado do retângulo nos nossos cálculos.
A soma de Riemann à direita para uma função num intervalo dividido em subintervalos é dada por:
onde e para .
Para a integral , temos , e .
Passo 2
Tabela:
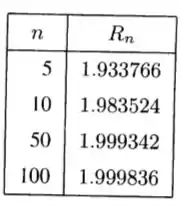
Os valores de parecem se aproximar de .