Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 44
Use as propriedades das integrais e o resultado do Exemplo 3 para calcular
Passo 1
Olá, meu querido amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Bom, vamos ter que resolver esta integral, mas antes vamos separar os termos, de acordo com a propriedade 4, ok?!
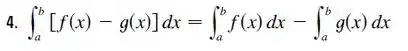
Passo 2
Então separando as integrais:
Usando a propriedade 3:
Então as constantes podem sair da integral:
Sabendo que:
Substituindo:
Nos intervalos:
Resposta
Exercícios de Livros Relacionados
Se f for contínuaem [a , b] , mostre que|int_a^b f (x) d x| = int_a^b |f (x)| d x [Sugestão: - |f (x)| = f (x) = |f (x)| .]
Use as propriedades das integrais para verificar a desigualdade sem calcular as integrais. 2 π 24 ≤ ∫ π 6 π 4 cos xd x ≤ 3 π 24
Demonstre a propriedade 6 das integrais.
Use a Propriedade 8 para estimar o valor da integral. ∫ 1 4 xd x
Use a Propriedade 8 para estimar o valor da integral. ∫ π 2 π x - 2 sen x d x