Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 5.2 - Ex. 6c
O gráfico de é apesentado. Estime com seis subintervalos usando
- Pontos médios
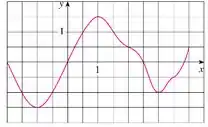
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Aqui a gente vai resolver essa integral
, infelizmente possuímos apenas o gráfico da função no intervalo solicitado
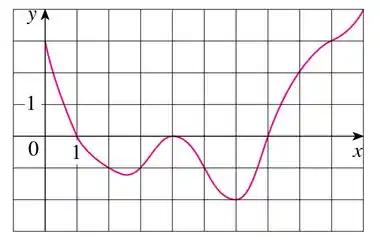
Isso nos coloca em uma posição de que a abordagem possa ser utilizando a soma de Rieman, pois é daí que vem as integrais.
Com ela, calculamos um somatório de pequenos retângulos abaixo do gráfico da região que queremos. Nessa questão vamos usar 5 subintervalos.
Para começar, vamos rever a fórmula da soma de Rieman,
Com
Onde é o número de subintervalos. é o comprimento de cada subintervalo e são os extremos do intervalo.
é um valor de que pertence ao subintervalo. Aqui vamos usar o ponto médio do subintervalo. Dessa forma, cada será calculado como:
Passo 2
Como temos um intervalo e queremos dividi-lo em subintervalos. Teremos que o comprimento de cada subintervalo será:
E,
Nossos intervalos e seus pontos médios são:
Logo, nossa extremidade esquerda são:
Em uma soma de Riemann com pontos médios, aproximamos a área usando retângulos em que a altura de cada retângulo é o valor da função no ponto médio esquerda de sua base e é a largura.
Logo,
Ou seja,
Olhando para o gráfico obtemos esses valores:
Logo,
Aqui vou colocar graficamente como ficaram representados os retângulos que usamos para fazer a soma de Riemann e quais foram os pontos da função que usamos para encontrar as alturas dos retângulos:
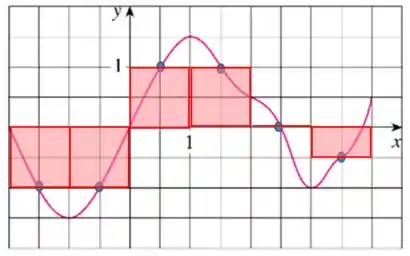
(Repare que o lado de cada quadradinho da grade do gráfico vale e isso pode causar estranhamento, mas sabemos disso por conta dos valores que são dados nos eixos e do gráfico).