Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.1 - Ex. 33

Use o cálculo para encontrar a área do triângulo com os vértices dados.

0,0 ,   3,1 ,   ( 1,2 )

Passo 1

Opa! Esse problema pede pra a gente calcular a área de um triângulo com as vértices:

0,0 ,   3,1 ,   ( 1,2 )

Pra isso a gente tem que usar nossos conhecimentos de cálculo!

Vamos começar colocando esses pontos no plano cartesiano:

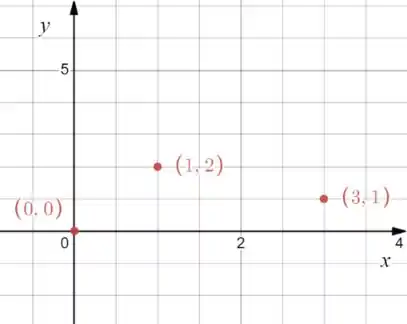
Vamos traçar 3 retas e vamos encontrar equações da reta com os pontos ! Fazendo com 0,0   e   3,1 .

Lembrando da equação reduzida da reta:

y - y 0 = m ( x - x 0 )

Para calcularmos o m:

m = y - y 0 x - x 0

Substituindo, temos

m = 1 - 0 3 - 0 = 1 3

y - 0 = 1 3 ( x - 0 )

Logo,

y = 1 3 x

Agora para os pontos 3,1   e ( 1,2 ) :

m = 2 - 1 1 - 3 = - 1 2

y - 1 = - 1 2 ( x - 3 )

y = - 1 2 x + 3 2 + 1

y = - 1 2 x + 5 2

Achamos a segunda, falta mais uma. Com 0,0   e   1,2 :

m = 2 - 0 1 - 0 = 2

y - 0 = 2 ( x - 0 )

y = 2 x

Passo 2

Plotamos o gráfico com as equações e obtemos:

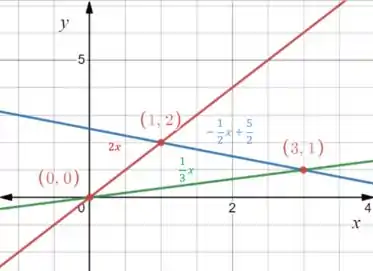
Nosso triângulo está pronto!! Vamos então calcular a área dele. Primeiro a gente subtrai a curva vermelha da verde e os limites de integração vão ser as intersecções x = 0 e x = 1 :

∫ 0 1 2 x - 1 3 x   d x

Agora a gente subtrai a reta verde da reta azul com os limites de integração x = 3 e x = 1 .

∫ 1 3 - 1 2 x + 5 2 - 1 3 x   d x

A área é a soma disso:

A = ∫ 0 1 2 x - 1 3 x   d x + ∫ 1 3 - 1 2 x + 5 2 - 1 3 x   d x

Reorganizando os termos da 2ª integral:

= 2 x 2 2 - 1 3 x 2 2 0 1   + ∫ 1 3 - 1 2 x + 5 2 - 1 3 x   d x

= 2 x 2 2 - 1 3 x 2 2 0 1   + ∫ 1 3 - 5 6 x + 5 2   d x

Pronto! Integrando real oficial:

= 2 x 2 2 - 1 3 x 2 2 0 1   + - 5 6 × x 2 2 + 5 2 x 1 3

Resolvendo:

= x 2 - 1 6 x 2 0 1   + - 5 12 × x 2 + 5 2 x 1 3

1 2 - 1 6 1 2 - 0 2 - 1 6 0 2   + - 5 12 3 2 + 5 2 3 - - 5 12 1 2 + 5 2 1

A = 1 - 1 6   + - 5 × 9 12 + 5 × 3 2 - - 5 12 + 5 2 = 5 2

Prontinho!!!

Resposta

A = 5 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios de 1 a 38 ache a área limitada pelas curvas dadas. Em cada problema, faça o seguinte: (a) desenhe uma figura mostrando a região e um elemento de área retangular; (b) expresse a área da
40. Ache por integração, a área do triângulo tendo vértices (3,4), (2,0), e (0,1).
39. Ache por integração, a área do triângulo tendo vértices (5,1), (1,3), e (-1,-2).
31. Ache a área da região limitada pela curva y x 2 + 1 3 = x 3 pelo eixo x, pelo eixo y e pela reta x = 1 .
32. Ache a área da região limitada pela curva y x 3 + 8 = 4 , pelo eixo x, pelo eixo y e pela reta x = 1 .