Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 6.7 - Ex. 28
Use um CAS para encontrar a massa e o centro de gravidade da lâmina dada de densidade .
A lâmina delimitada por , , e ; .
Passo 1
A ideia aqui é encontrar a massa pela expressão:
Já que a densidade é constante. E encontrar o centro de gravidade usando nossas fórmulinhas:
Vamos começar!
Passo 2
Primeiro, vamos achar a área da nossa lâmina:
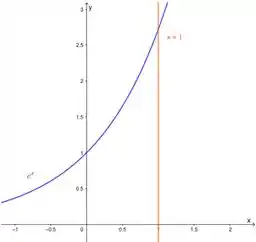
A região descrita por ela é limitada por cima pela função e por baixo pela função . E ela está no intervalo .
Podemos então dizer que a área pode ser achada pela integral:
Então a massa é:
Passo 3
Vamos achar as coordenadas do centro de gravidade por integração. Primeiro a coordenada :
No eixo , nossa região está entre (por cima) e (por baixo). E em , entre e .
Substituindo tudo, nossa integral fica:
Usando um CAS para resolver a integral (a gente vai usar aqui a calculadora CAS do Geogebra, que dá para acessar pelo navegador):
Passo 4
Agora a coordenada . A gente pode usar essa fórmula aqui:
No eixo , nossa região está entre (por cima) e (por baixo). E em , entre e .
Substituindo tudo, nossa integral fica:
Usando um CAS para resolver a integral (lembrando que gente vai usar aqui a calculadora CAS do Geogebra, que dá para acessar pelo navegador):
Temos que o nosso centro de gravidade está no ponto: