(a) Use um CAS para mostrar que, se for uma constante positiva, então
(b) Confirme esse resultado usando a regra de L’Hôpital. [Sugestão: Expresse o limite em termos de .]
(c) Se for um inteiro positivo, então segue por (a) com que a aproximação
deveria ser boa com grande. Use esse resultado e a tecla da raiz quadrada de uma calculadora para aproximar os valores de e com e, então, compare os valores obtidos com aqueles do logaritmo gerados diretamente da calculadora. [Sugestão: Cada raiz enésima na qual é uma potência de dois pode ser obtida como sucessivas raízes quadradas.]
Passo 1
(a) O que a gente precisa fazer é calcular esse limite usando o CAS. Vamos usar o Wolfram Mathematica para fazer essa continha. Fica assim:
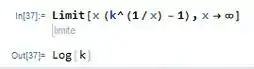
Como o enunciado disse, realmente dá .
Passo 2
(b) Agora vamos tentar chegar nesse resultado usando a regra de L’Hospital e a sugestão do enunciado. Precisamos fazer a substituição:
O limite fica assim:
Vamos usar L’Hospital nele. Só derivar em cima e embaixo separadamente:
Chegamos no mesmo resultado que o CAS. Uhul!
Passo 3
(c) Precisamos usar a aproximação:
Com , ou seja:
Para calcular e . E depois comparar o que a gente achar com os valore reais.
Maaas, a gente só pode usar a raiz quadrada. Então em vez de calcularmos direto, vamos calcular a raiz quadrada de dez vezes consecutivas. Porque aí chegamos em
Belezinha? Vamos começar!
Passo 4
Precisamos achar . Então vamos usar a aproximação com . Fica assim:
Calculando esse log direto, achamos . A aproximação que a gente usou deu um resultado bem legal.
Vamos fazer o mesmo com . Se :
Calculando esse log direto, achamos . De novo, a aproximação foi boa. Chegou a acertar três casas decimais.
Que bonita a matemática, né? haha
Resposta
- Prova nos passos
- Prova nos passos
- , ,