Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 47
Use cascas cilíndricas para encontrar o volume do sólido.
Um cone circular reto de altura e base com raio .
Passo 1
Para calcularmos o volume do sólido de rotação em torno do eixo da região sob a curva de até é
Então, para o cone, temos:
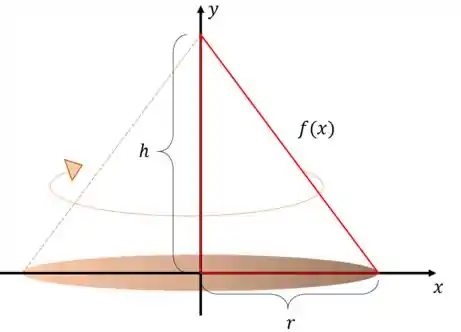
Passo 2
Como a função é a reta que passa pelos pontos e , sua equação é dada por:
Onde
Então:
Para o ponto :
Então a reta é dada pela equação:
Passo 3
Então, queremos o volume da rotação de de a :
Resposta
Exercícios de Livros Relacionados
Escreva, mas não calcule, uma integral para o volume de um sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo especificado. x 2 - y 2 = 7 ,x = 4 ; em torno de y = 5
Use o método das cascas cilíndricas para achar o volume gerado pela rotação da região delimitada pelas curvas dadas em torno do eixo especificado. Esboce a região e uma casca típica. y = 4 x - x 2 ,y
Escreva, mas não calcule, uma integral para o volume de um sólido obtido pela rotação da região limitada pelas curvas dadas em torno do eixo especificado. y = 1 1 + x 2 ,y = 0 ,x = 0 ,x = 2 ; em torno
Use a Regra do Ponto Médio com n = 5 para estimar o volume obtido pela rotação em torno do eixo y da região sob a curva y = 1 + x 3 ,0 ≤ x ≤ 1 .
A região delimitada pelas curvas dadas é girada em torno do eixo especificado. Ache o volume do sólido resultante por qualquer método. x 2 + y - 1 2 = 1 ; em torno do eixo y