Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 27
Use a Regra do Ponto Médio com para estimar o volume obtido pela rotação em torno do eixo da região sob a curva .
Passo 1
Esboçando o enunciado temos o seguinte desenho:
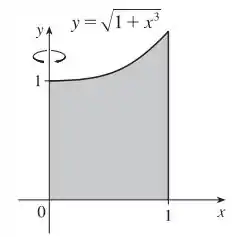
Passo 2
Como a função gira em torno do eixo e ela já está em , nosso raio é o próprio , e nossa altura é a função , então nossa integral é:
Passo 3
Dizendo que nossa função é , e usando a Regra do Ponto Médio em , temos
Multiplicando por ,que é a parte do volume que foi deixada de fora temos um que vale mais ou menos .
Resposta
.
Exercícios de Livros Relacionados
44- Deduza a equação do volume de uma esfera de raio r usando o método da casca.
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 28 – A – O eixo x.
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 27 – C – A reta y = 8 5 .
Nos Exercícios 27 e 28, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados. 27 – D – A reta y = - 2 5 .
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.26 - y = x 4ey = 4 - 3 x 2 B