Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 6.3 - Ex. 45
Use as cascas cilíndricas para encontrar o volume do sólido. Uma esfera de raio .
Passo 1
Fala ai, galerinha! 😁
Nesse problema temos que usar o método das cascas cilíndricas para obter o volume da esfera de raio .
Tem ideia de como fazemos isso? 😐
O método das cascas cilíndricas é um método para calcular o volume de um sólido de revolução, ou seja, um sólido obtido pela rotação de uma região plana em torno de um eixo.
Esse método consiste em dividir o sólido em cascas cilíndricas, que são cilindros com espessura muito pequena, e somar os volumes dessas cascas. O volume de uma casca cilíndrica pode ser calculado pela fórmula:
Onde é o volume da casca cilíndrica, é o raio médio da casca cilíndrica, é sua altura e é sua espessura.
Para aplicar o método das cascas cilíndricas, é preciso identificar o raio e a altura da casca cilíndrica em função de uma variável, geralmente ou , e integrar a expressão do volume de até , que são os limites da região plana. A fórmula geral do volume de um sólido de revolução pelo método das cascas cilíndricas é:
Parece de boa? 👀
Passo 2
Temos o seguinte esboço para esse caso...
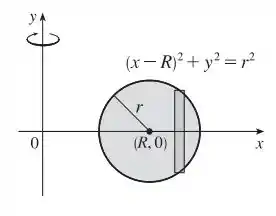
Com isso, conseguimos achar nossa fórmula. A nossa função varia de até , então:
Para facilitar os cálculos, diremos que :
A primeira integral é a área de um semicírculo de raio , que é , e a segunda é , porque integrando teremos uma função ímpar. Assim, temos:
E aí! O que achou? Responde Aí! 😬
Resposta
.