Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 78
Use um computador para investigar a família de superfícies
Como a forma do gráfico depende dos números e ?
Passo 1
Eaee, belezinha?? Bom... queremos utilizar um software matemático para plotar várias funções no seguinte formato:
Onde e são constantes.
Aqui a gente vai aplicar alguns valores de e e ir plotando. Com isso, iremos analisar o que acontece quando alteramos os valores de e , certinho??
Para ser mais específico e ficar melhor de entendermos, vamos primeiramente fixar um valor de e alterar os valores de .
Em seguida vamos fazer o contrário. Por fim, vamos adotar valores iguais para e .
Agora bora lá!! 😉
Passo 2
Vamos fazer o seguinte, com , vamos traçar alguns gráficos para diferentes valores de .
Para :
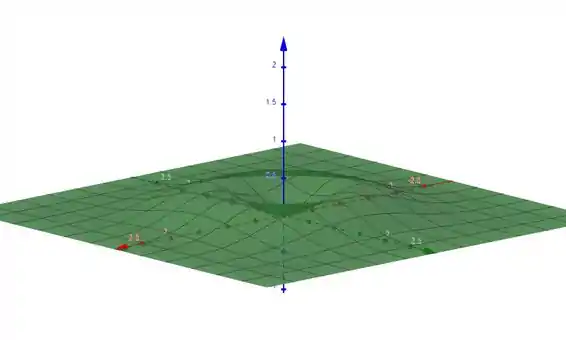
Para :
Para :
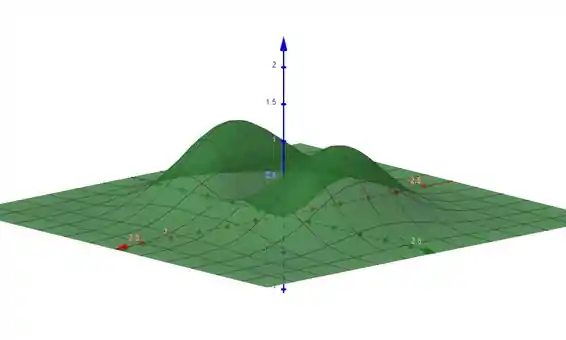
Passo 3
Agora mantendo e variando .
Para :
Para :
Passo 4
Agora com :
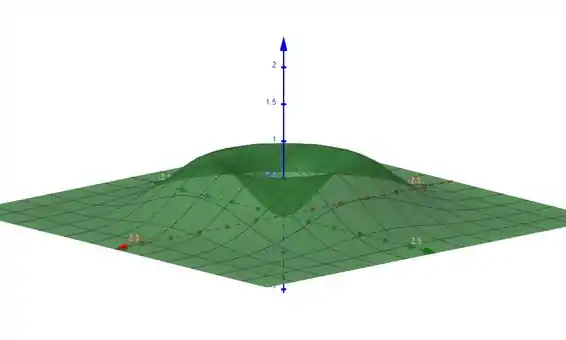
Com e :
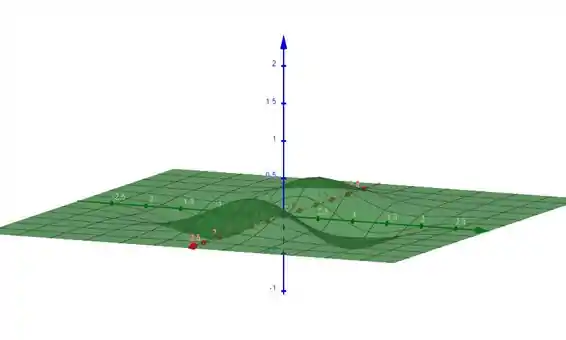
Passo 5
Podemos perceber que com o aumento de ou o pico da função aumenta a altura.
Se tivermos , temos um circulo inteiro como máximo da função, ou mínimo se , quando temos dois picos de mesma altura, sobre o eixo e se temos o mesmo, mas sobre o eixo .
Se um dos dois valores for negativo, vamos para baixo do plano e temos vales, da mesma maneira, se temos um circulo inteiro de mínimo da função, se , como estamos falando de valores negativos, os vales estarão no eixo e da mesma forma se os vales estarão no eixo .
Resposta
Comentários