Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.1 - Ex. 74

Utilize um computador para traçar o gráfico da função, utilizando vários pontos de vista e tamanhos de janela. Imprima aquela que apresente melhor os “picos e vales”. Você acha que essa função tem um valor máximo? Você poderia identificar os pontos do gráfico correspondentes aos “máximos locais”? E aos “mínimos locais”?

Passo 1

Olá, meu querido estudante. Pronto para mais uma resolução?

A gente tem a função:

E iremos produzir seu gráfico utilizando um software gráfico. Devemos também discutir sobre o valor máximo dessa função, além de identificar os máximos locais e mínimos locais.

Máximos e mínimos locais são pontos em um gráfico de uma função onde a função atinge valores máximos ou mínimos em relação aos pontos próximos a eles. Os máximos e mínimos locais são relativos aos pontos próximos, enquanto os globais são relativos a todo o domínio da função.

Então iremos plotar o gráfico dessa função utilizando o GeoGebra, por ser um software gráfico gratuito e online.

Nele iremos analisar os picos e vales da nossa função, e iremos analisar se o comportamento do gráfico da função permite crescimentos e decrescimentos após os picos e vales que encontrarmos.

Passo 2

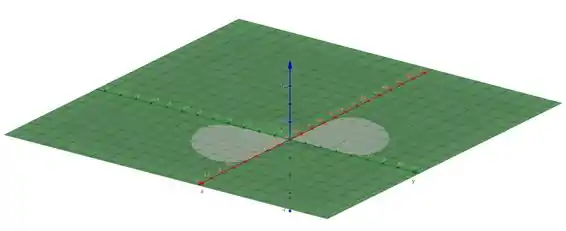
Traçando o gráfico e analisando diversos ângulos, o que melhor representa os máximos da função é

De longe vemos nossa figura assim:

Com o eixo em nossa direção:

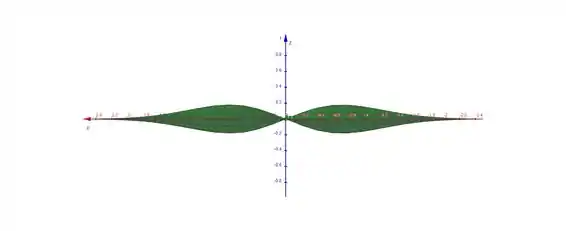
Vemos que de fato a primeira opção é a melhor para visualizar o comportamento do gráfico, mas não que as outras não ajudem a visualizar o mesmo.

Passo 3

Podemos claramente indicar que os picos, ou máximos locais, da função que são esses dois

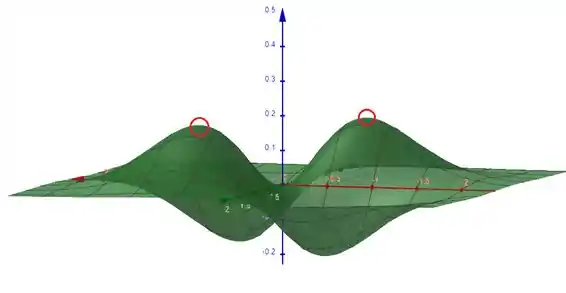
Já para vales ou mínimos, são esses outros dois

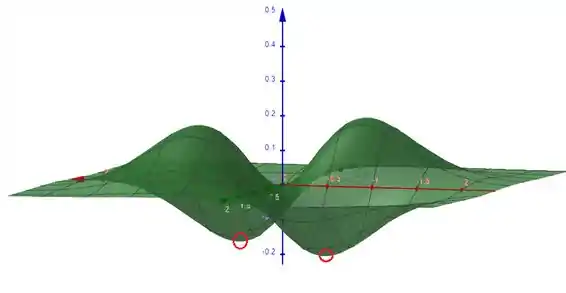
Pelo que podemos ver, muito provavelmente a função possui valor máximo, o comportamento do gráfico não indica que exista um crescimento ‘infinito’ após esses dois picos.

Resposta

Picos

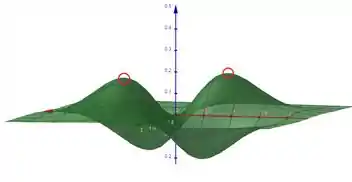
Vales

Pelo que podemos ver, muito provavelmente a função possui valor máximo, o comportamento do gráfico não indica que exista um crescimento ‘infinito’ após esses dois picos.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Exercício de Livro

Faça um esboço do diagrama de contorno da função cujo gráfico é mostrado.

(a) Mostre que, tomando logaritmos, a função geral de Cobb-Douglas P = b L α K 1 - α pode ser expressa como ln ⁡ P K = ln ⁡ b + α ln ⁡ L K (b) Se tomarmos x = ln ⁡ L K e y = ln ⁡ P K , a equação da pa

Seja f x , y = x x 2 + y 2 . Desenhe a imagem da curva γ t = ( x t , y t , z t ) , onde x t = Rc o s t ,y t = Rs e n t e z = f ( x , y ) (R0) . Como é o gráfico de f ?

10. Sejam f x , y = x yeγ t = a t , b t , f a t , b t . Desenhe a imagem de γ sendoa) a = 0 e b = 1 . b) a = 1 e b = 1 . c) a = 1 e b = 0 . d) a = - 1 e b = 1 .