Desenhe as curvas de nível e determine a imagem.
Passo 1
Igualamos
Passo 2
Obter a equação das curvas de nível a partir de diferentes valores de c:
Passo 3
Esboçar as curvas de nível partir das equações:
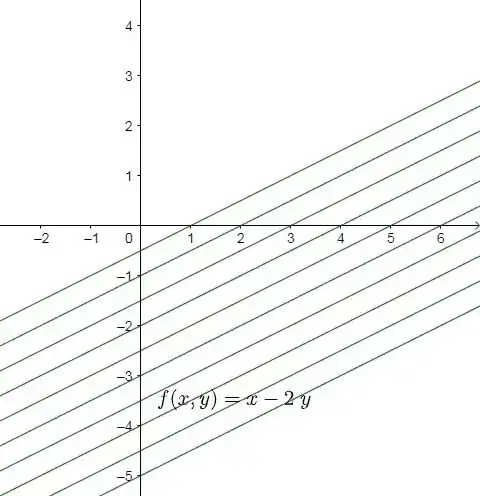
Im f = IR
Resposta
Ei, a resposta está no passo a passo :)