Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 5.4 - Ex. 49
Use a Definição 5.4.3 tomando como a extremidade direita de cada subintervalo para encontrar a área líquida sob a curva acima do intervalo especificado.
confira sua resposta com um argumento geométrico simples.
Passo 1
Segundo a definição 5.4.5, a área líquida entre a curva de em , em é dada por:
Onde sendo calculada pela extremidade direita, a gente faz:
Trazendo isso pro nosso caso então, temos:
Passo 2
Vamos aplicar na fórmula da área então:
Vamos separar e calcular os somatórios agora...
Passo 3
Beleza, vamos ver por que a área deu zero...
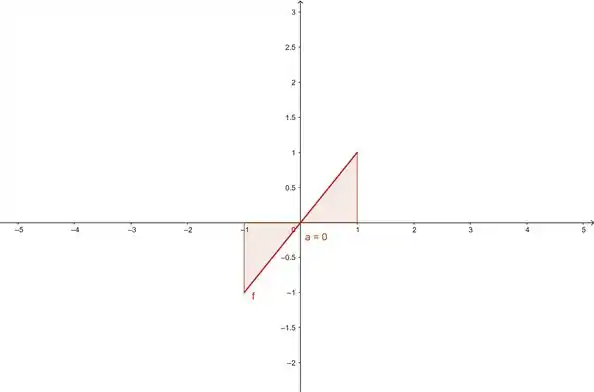
Olha aí! A parte positiva é igual a parte negativa! Ou seja, as áreas se anulam, gerando uma área líquida igual a zero😉
Resposta
Exercícios de Livros Relacionados
72. Se F ( x ) = ( x 2 + 3 x + 2 ) / ( 2 - | x | ) .a. Faça tabelas de valores de F para os valores de x que se aproximam de x 0 = - 2 por cima e por baixo. Em seguida, estime lim x → - 2 F ( x ) c.
71. Se ( x ) = ( x 2 - 1 ) / ( | x | - 1 ) .a. Faça tabelas de valores de f para os valores de x que se aproximam de x 0 = - 1 por cima e por baixo. Em seguida, estime lim x → - 1 f ( x ) c. Determi
79. Se lim x → 4 f x - 5 x - 2 = 1 , determine lim x → 4 f ( x )
78. Suponha que g x ≤ f x ≤ h ( x ) para qualquer x ≠ 2 , e suponha que lim x → 2 g ( x ) = lim x → 2 h ( x ) = - 5 Podemos concluir algo com relação aos valores de f, g e h em x = 2 ? É possível
76. Seja f ( x ) = ( 3 x - 1 ) / x .a. Faça uma tabela dos valores de f em valores de x que se aproximam de x 0 = 0 por cima e por baixo; f parece ter um limite quando x → 0 ? Em caso afirmativo, qual