Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 2.2 - Ex. 72
72. Se .
a. Faça tabelas de valores de para os valores de que se aproximam de por cima e por baixo. Em seguida, estime
c. Determine algebricamente.
Passo 1
a.
Para fazermos essa tabela, só precisamos ir jogando os valores, cada vez mais próximos de , na fórmula e ver para onde está tendendo:
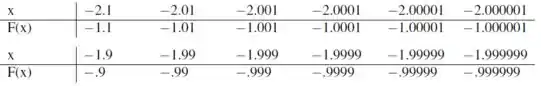
Podemos observar que está se aproximando de
tanto por cima quanto por baixo.
Passo 2
c.
Vamos analisar a função :
Se , então:
Mas, se :
Para
Como o limite está tendendo a , vamos usar a para quando . Com isso podemos calcular facilmente que
Resposta
a.
c.
Exercícios de Livros Relacionados
Use a Definição 5.4.3 tomando como a extremidade direita de cada subintervalo para encontrar a área líquida sob a curva y = f ( x ) acima do intervalo especificado. f x = x ,- 1,1 , confira sua respos
Use a Definição 5.4.3 tomando como x k * como o ponto médio de cada subintervalo para encontrar a área sob a curva y = f ( x ) acima do intervalo especificado. f x = 2 x ;0 , 4
Use a Definição 5.4.3 tomando como a extremidade esquerda de cada subintervalo para encontrar a área sob a curva y = f ( x ) acima do intervalo especificado. f x = 5 - x ; 0,5
Use a Definição 5.4.3 tomando como a extremidade direita de cada subintervalo para encontrar a área líquida sob a curva y = f ( x ) acima do intervalo especificado. f x = x ,- 1,2 , confira sua respos
Use a Definição 5.4.3 tomando como x k * como o ponto médio de cada subintervalo para encontrar a área sob a curva y = f ( x ) acima do intervalo especificado. f x = x 2 ;0,1