Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 10.5 - Ex. 52
Use a definição de uma hipérbole para deduzir a Equação 6 para uma hipérbole com focos e vértices .
Passo 1
Olá, meu amigo. Tudo bem?! Estarei te ajudando a resolver essa atividade.
A Equação 6 que precisamos deduzir é
Pela definição de hipérbole, sabemos que , onde é um ponto qualquer pertencente a hipérbole.
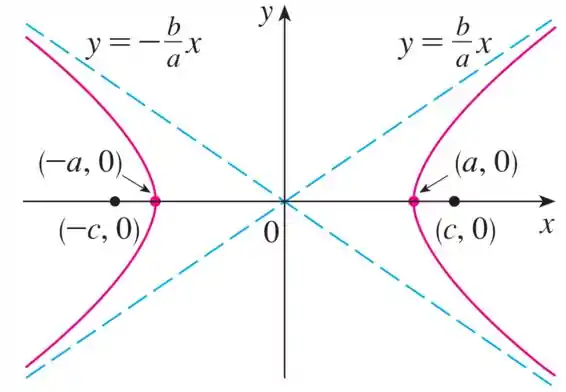
Vamos visualizar melhor a forma dessa equação num gráfico:
Passo 2
Então, usando a fórmula para distância entre dois pontos, ficamos com:
Elevando os dois lados da equação ao quadrado:
Vamos lembrar de um produto notável agora: e aplicá-lo na nossa conta:
Agora elevamos ao quadrado dos dois lados mais uma vez:
Lembra que ? Agora olha pra nossa equação, esse termo aparece ali duas vezes, vamos substituí-los:
Agora vamos dividir a equação toda por :
E assim, terminamos nossa demonstração.
Resposta
Ver o desenvolvimento.