Faça o esboço de um campo de direções para a equação diferencial autônoma , onde o gráfico de f é como o exibido. Como o comportamento-limite das soluções depende do valor de ?
Passo 1
Precisamos fazer o esboço de um campo de direções baseado no gráfico que nos foi dado, vamos notar que existem soluções de equilíbrio em . Isso quer dizer que os declives nesses pontos são (constantes).
Quando a curva está acima do eixo em , os campos de direção são positivos e, portanto, apontam para cima; da mesma forma, quando a curva está abaixo do eixo em , as inclinações apontam para baixo. Quanto mais longe os campos de direção são das linhas de equilíbrio, mais íngremes eles são.
A partir dessas observações, podemos desenhar o seguinte campo:
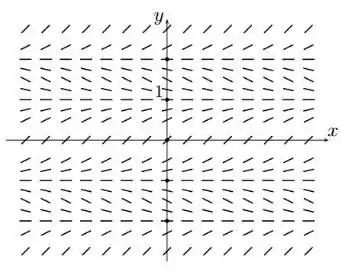
Resposta
Ei, a resposta está no passo a passo :)