Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 2.2 - Ex. 46
- A partir do gráfico da função
E dando zoom o ponto em que o gráfico cruza o eixo , estime o valor de
- Verifique sua resposta do item (a) calculando para valores de que tendam a zero
E dando zoom o ponto em que o gráfico cruza o eixo , estime o valor de
Passo 1
Eaeee, belezinha??
Bom... queremos determinar o seguinte limite:
Mas para isso o enunciado que a gente fique dando zoom no ponto em que o gráfico cruza o eixo de forma que este valor que queremos seja estimado.
Depois a gente vai substituindo por valores que se aproximam de na função para confirmar a nossa estimativa.
Agora bora lá!! 😉
Passo 2
Esboçando o gráfico e dando zoom com o auxilio de uma ferramenta gráfica, ficamos com
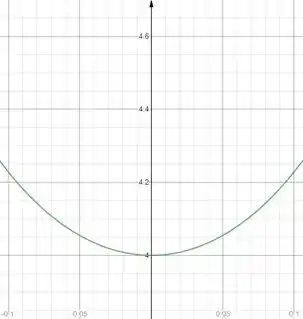
E a partir do gráfico, podemos concluir que
Show?
Passo 3
Para o item b), construindo uma tabela com valores de tendendo a zero e confrontando com seus respectivos .
Por exemplo
Logo, se aproximando de , temos
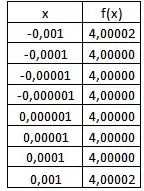
E a partir da tabela, podemos concluir que
Entendeu direitinho?? Responde Aí! 😉