Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 20
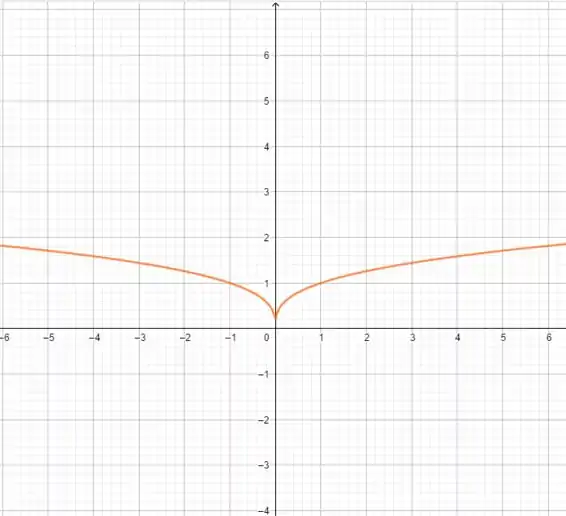
(a) Use o gráfico de para ajudar a esboçar o gráfico de .
(b) Use o gráfico de para ajudar a esboçar o gráfico de .
Passo 1
Cara, nas duas letras, temos que colocar o módulo em , ou seja, . Agora, pensa comigo, o que isso faz? A função módulo transforma todos os valores negativo em positivos e não muda nada nos que já são positivos.
Dessa forma, em uma raiz quadrada, agora, todos os valores de passarão a ser válidos. Isso porque os positivos já eram e, com o módulo, os valores negativos de passarão a ser positivos, logo, validados no domínio de . Ok? Então, nesse gráfico, a diferença é que teremos o espelho do que acontecia para valores positivos nos valores negativos:
(a)
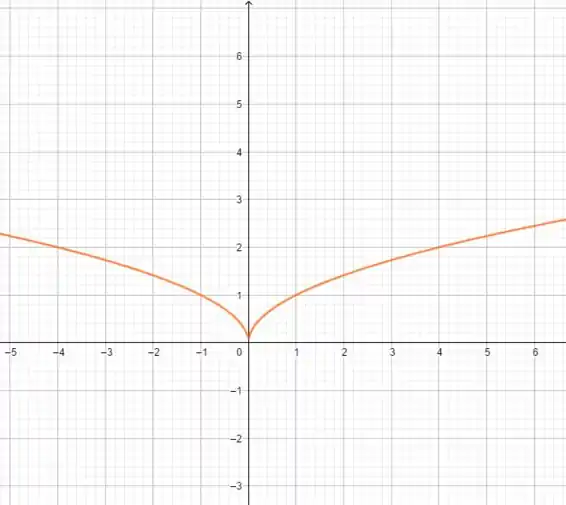
Pegamos o que acontecia para e repetimos para , ok?
Passo 2
Para , vamos apenas espelhar pelo eixo o gráfico para . Pois, com o módulo, todos os valores serão positivos, ou seja, faremos para . E essa multiplicação por espelha o gráfico pelo .
Olha a diferença entre :
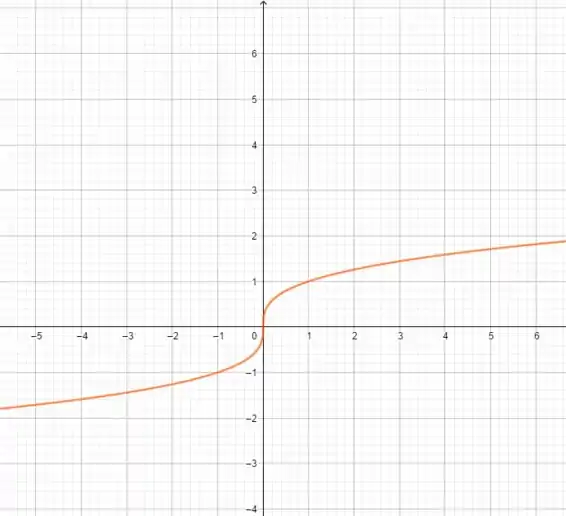
Para :
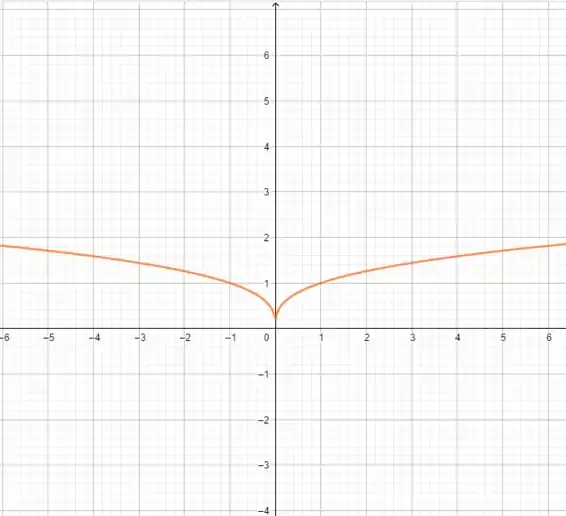
Os dois gráficos ficaram iguais haha 😊
Resposta
(a)
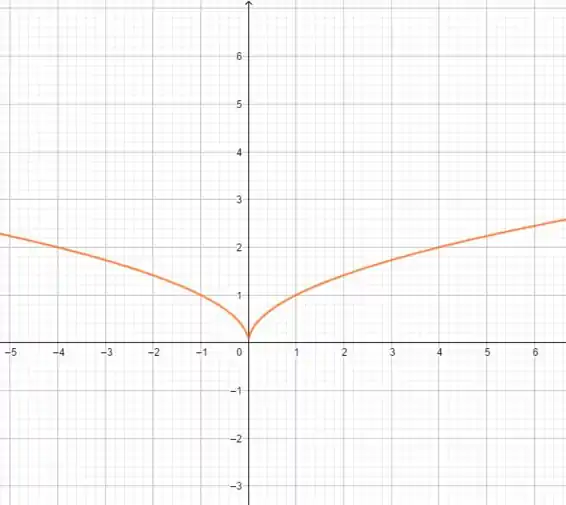
(b) 