Segue a partir da Lei da Gravitação Universal de Newton que o peso de um objeto, em relação à Terra, é inversamente proporcional ao quadrado da distância entre o objeto e o centro da Terra, isto é, .
(a) Supondo que um satélite meteorológico pese 900 kg na superfície da Terra e que a Terra seja uma esfera com raio de 6400 km, ache a constante C.
(b) Encontre o peso do satélite quando estiver 1600 km acima da superfície da Terra.
(c) Faça um gráfico do peso do satélite versus sua distância ao centro da Terra.
(d) Há alguma distância do centro da Terra na qual o peso do satélite seja zero? Explique seu raciocínio.
Passo 1
(a) Se a força é inversamente proporcional ao quadrado da distância, nós temos essa relação entre elas:
Podemos isolar a constante:
Como temos e :
Passo 2
(b) Aqui, vamos apenas usar a fórmula:
Queremos , se :
Passo 3
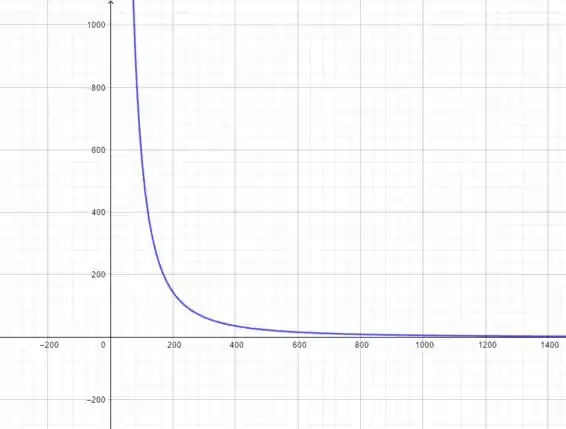
(c) Para fazer o gráfico da força versus distância, vamos plotar a fórmula.
O gráfico fica assim:
Passo 4
(d) Pelo gráfico, a gente pode ver que quanto mais perto o objeto está do centro da Terra, maior será o peso. O problema é que temos uma assíntota vertical em , pois temos uma divisão por :
E, conforme afastamos o objeto, peso diminui, tendendo a Mas nunca chega a , isso porque para ele ser , a constante deveria ser nula!
E isso bate com a proporcionalidade que vimos lá no início: o peso é inversamente proporcional ao quadrado da distância.
Resposta
(a)
(b)
(c) 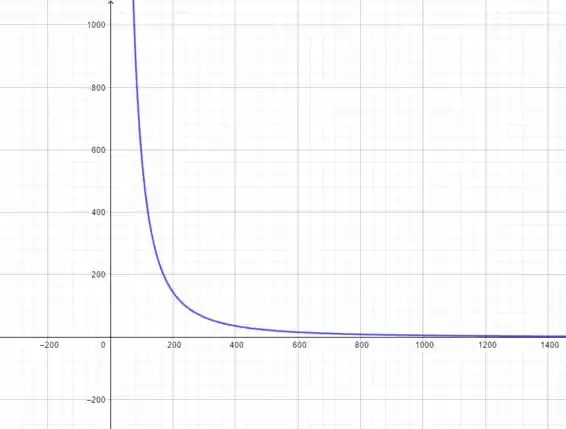
(d) Não, para isso, a constante deveria ser nula.