Use um gráfico do campo vetorial e a curva para dizer se a integral de linha de ao longo de é positiva, negativa ou nula. Em seguida, calcule a integral.
, é o arco de círculo percorrido no sentido anti-horário de a .
Passo 1
Vamos lá, o enunciado nos deu várias informações . Então vamos começar tentando entender o que ele quer.
Ele nos deu um campo vetorial e uma curva e quer que façamos uma análise gráfica que nos diga como será o comportamento da integral de linha ao longo dessa curva .
Depois iremos ter que achar esse comportamento realizando a integral de linha de fato.
Então a primeira coisa que temos que entender é como esboçar o gráfico do campo vetorial F e a curva C.
Passo 2
Vamos começar pelo arco C . Eles nos diz que esse arco pertence a um círculo .
A forma padrão para representar um círculo é a seguinte:
Logo podemos dizer que o raio da equação do círculo que ele nos deu irá ser , e o irá ser . Construindo o círculo teremos a figura abaixo:
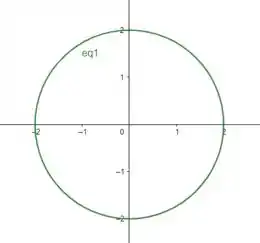
Porém, ele quer que a curva percorra do ponto a , no sentido anti-horário.
Ou seja, não teremos o quarto quadrante do círculo, porque não está incluso do ponto a . Logo a curva será representada por :
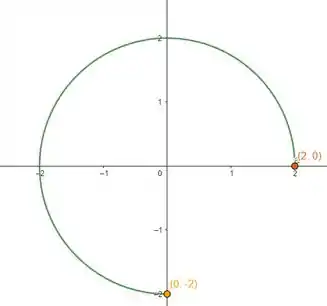
Passo 3
Beleza, agora precisamos construir o campo vetorial.
Vamos precisar de uma informação que ele nos dá lá no enunciado.
Show, para construir o campo vetorial precisamos supor alguns pontos para entendermos qual é o seu comportamento. Bom , esses pontos são aleatórios ?
SIM E NÃO…..
Podemos sim escolher qualquer ponto para desenharmos o campo vetorial porém para sermos mais assertivos precisamos escolher pontos que tenham alguma conexão com o nosso problema.
Por exemplo, vou supor os seguintes pontos:
, ,,
Esses são pontos que pertencem ao meu arco :
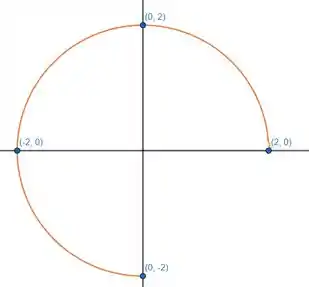
Agora, iremos substituir cada ponto lá em função do campo vetorial.
Para o ponto
Para o ponto
Para o ponto
Para o ponto
Beleza , agora se olharmos os resultados , no caso desses pontos, o vetor vai variar 2 unidade no eixo . Vamos desenhá-los :
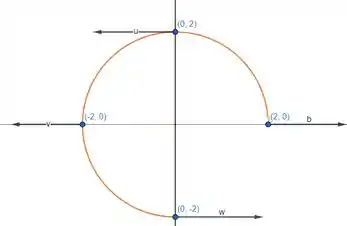
A partir desses vetores podemos observar um pouco do comportamento . Vemos que eles seguem o sentido anti-horário apontando a mesma direção da curva . Então isso nos leva a crer que a linha integral de linha será positiva.
Porém o campo vetorial completo pode ser mais trabalhoso de ser desenhado manualmente , então podemos desenhá-lo utilizando um software.
Utilizando um software obtemos o seguinte resultado:
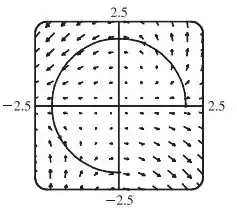 .
.
Passo 4
Beleza, nós conseguimos entender o comportamento da integral apenas com o campo de força e com a curva, mas o exercício nos pede para confirmar esse resultado fazendo uma integral.
Então vamos nessa!!!
Já sabemos que a curva será o arco do círculo percorrido no sentido anti-horário de a .
A curva será os intervalos da nossa integral. Porém como ela é um arco de um círculo ,ela irá variar de acordo com os ângulos e a nossa função está variando em , então não vai dar bom
Por isso iremos fazer uma parametrização.
O primeiro passo para parametrizar é escolher um parâmetro, vamos usar o , já que os nossos intervalos serão ângulos.
O segundo passo será definir os intervalos. Como vimos anteriormente a nossa curva tem o seguinte aspecto:
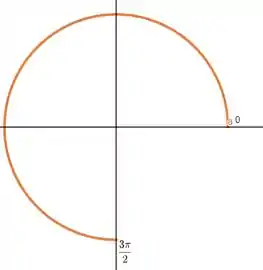
Podemos ver que o varia de a . Logo nosso intervalo será:
O terceiro passo vai ser achar a equação paramétrica. Nesse tipo de exercício é muito comum utilizar as coordenadas polares. Assim , podemos dizer que nossa equação será:
Aonde serão representados sendo :
Passo 5
Beleza agora que já sabemos como funciona a parametrização vamos substituir os valores.
Lembra que o ??
Então podemos substituir esse valor e termos que :
Agora vamos substituir o e o lá no campo vetorial que ele nos deu. Lembra??
Vai ficar assim:
Passo 6
Essa questão é um pouquinho grande mas calma que está quase acabando. Lembrando que nosso objetivo aqui é realizar a integral de linha .
Mas para isso precisávamos descobrir quem era e , como foi feito nos passos anteriores.
A função já sabemos que será :
Agora vamos achar :
Derivando teremos :
Passo 7
Agora fazer o produto escalar entre :
=
=
Passo 8
Belezinha, esse resultado é o que vamos integral, sendo assim :
Podemos separar em 3 integrais para ficar mais fácil
Vamos começar pela primeira :
Nesse caso iremos precisar fazer uma integral por substituição , vai ficar assim:
substituindo na integral :
Passo 9
Vamos para a segunda integral :
Para fazer essa integral a gente pode usar um bizu . Lembra da equação para arco duplo?
Substituindo na integral:
Vamos dividir em duas partes:
Mais uma vez vai ser necessária fazer a integral por substituição:
Substituindo na integral :
2
Passo 10
Ufa, agora vamos para última integral :
vamos utilizar o método de substituição:
iremos chamar e
Para não ficar negativo podemos trocar os limites de integração
Passo 11
Beleza , agora temos os valores de cada integral que separamos lá no início :
Substituindo o resultado de cada uma teremos :
O resultado deu positivo, como previmos.