Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.2 - Ex. 28
Use um gráfico do campo vetorial e a curva para dizer se a integral de linha de ao longo de é positiva, negativa ou nula. Em seguida, calcule a integral.
é a parábola de a .
Passo 1
E aiii minha turma, beleza?!
Devemos usar um gráfico do campo e a curva C nesse mesmo gráfico, para dizer se a integral de linha de F ao longo de é: negativa, positiva ou nula.
é a parábola de a .
Feito isso, devemos calcular o valor da integral.
Por onde começamos?
O primeiro passo é esboçar o campo , e representar a parábola indicando o caminho de a . Fazendo isso com o auxílio do Geogebra, temos:
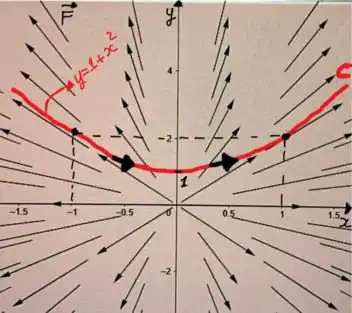
Agora avalie com calma esse gráfico, observe bem o sentido do vetor F e do caminho percorrido, começando em e indo até . Uma dica, o campo F é simétrico no primeiro e segundo quadrante.
Para calcular a integral de linha, devemos lembrar como ela é escrita. Assim temos que:
Observe que precisamos encontrar uma parametrização para nossa curva .
Sabemos que:
Uma parametrização aceitável é chamarmos , assim ficamos com:
Dessa forma nosso vetor , fica:
Observe uma coisa, se você aplicar e , você vai encontrar exatamente os pontos dado no enunciado. O que indica que essa parametrização está de acordo.
Agora não tem erro, é só aplicar na integral e fazer o produto escalar. Lembre-se de parametrizar o campo , fazendo .
Conforme recomendação do livro, utilize um software para calcular a integral de linha.
Vamos lá!!
Passo 2
Vamos começar avaliando o gráfico e tentar afirmar se é a integral de linha é: positiva, negativa ou nula.
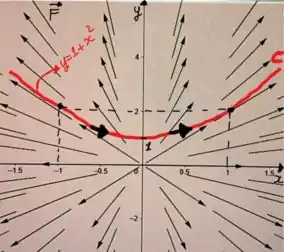
Observe o seguinte:
Começando em , no segundo quadrante, à medida que vamos descendo a curva as setas dos vetores parecem estar apontadas justamente no sentido oposto do caminho.
Mas, quando chegamos no ponto mais baixo da parábola, isso se inverte. À medida que subimos a curva, as setas parecem acompanhar o sentido do caminho.
Como existe simetria entre as duas partes, é razoável supor que a integral deve ser nula.
Passo 3
Vamos calcular a integral de linha e verificar se realmente ela é nula.
Sabemos que:
Vimos que uma parametrização adequada para a parábola pode ser representada por:
Nosso campo é:
Vamos achar . Aplicando no campo , vamos ter:
Por fim, só faltou achar . Derivando em relação a , vamos obter:
Passo 4
Podemos então escrever a integral assim:
Aplicando o produto escalar, vamos ter:
Simplificando um pouco, ficamos com:
Utilizando o WolframAlpha com o seguinte input: Integrate[(3t+2t^3)/Sqrt[(t^4+3t^2+1)],{t,-1,1}]
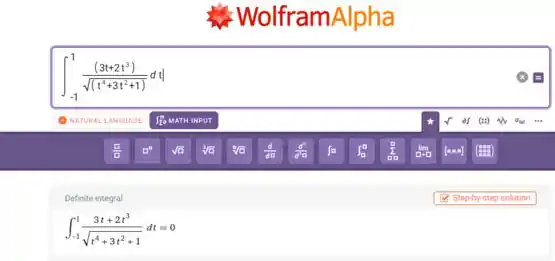
Observe que realmente deu zero, como previmos por meio do gráfico.