Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diomara - Cálculo Diferencial e Integral de Funções de Várias Variáveis- Ed: 3º - Capítulo 6.3 - Ex. 4d

4. Calcule

int_C F * d vec r

Onde

d. F (x , y) = (x^2 + y^2 , x^2 - y^2) e C é a curva de equação y = 1 - |1 - x| de (0,0) a (2,0)

Passo 1

OIII , estamos na seção agora de integrais de linha em campo vetorial. Pra mim é mais fácil que campo escalar, porque não precisamos tirar modulo das nossas parametrizações. Então temos um passo a menos. Quando temos uma integral de linha podemos fazer uma parametrização para deixá-la mais simples

int_C F * d vec r

Logo se dissermos que

r = gamma (t)

d r = gamma^' (t) d t

Assim, nossa integral parametrizada fica no seguinte formato

int_C F * d vec r = int_(t_0)^(t_1) F (gamma ( t )) * gamma^' (t) d t

Bora cair dentro !!!! \o/

Passo 2

No nosso caso temos que C é a curva de equação y = 1 - |1 - x| de (0,0) a (2,0) . Função com modulo é sempre estranha. Vamos olhar para o gráfico dessa curva

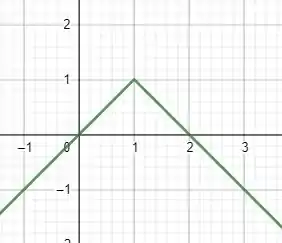
Parametrizar isso não será tão trivial. O mais prático será quebrar o modulo e repartir o intervalo da nossa integração em 2. Entao nossa parametrização sera

gamma_1 (t) = (t , t)

gamma_1^' (t) = (1 , 1)

t in [0,1]

Agora nossa segunda parametrização

gamma_2 (t) = (t , 2 - t)

gamma_2^' (t) = (1 , - 1)

t in [1 , 2]

Show!!! Já conseguimos boa parte do processo, agora só falta parametrizar nossa função

F (x , y) = (x^2 + y^2 , x^2 - y^2)

F (gamma_1 (t)) = (t^2 + t^2 , t^2 - t^2)

F (gamma_1 (t)) = (2 t^2 , 0)

F (gamma_2 (t)) = (t^2 + (2 - t)^2 , t^2 - (2 - t)^2)

F (gamma_2 (t)) = (2 t^2 + 4 - 4 t , - 4 + 4 t)

Passo 3

Bora integrar!

int_C F * d vec r = int_(t_0)^(t_1) F (gamma ( t )) * gamma^' (t) d t

= int_0^1 (2 t^2 , 0) * (1,1) d t + int_1^2 (2 t^2 + 4 - 4 t , - 4 + 4 t) * (1 , - 1) d t

= int_0^1 2 t^2 d t + int_1^2 ( 2 t^2 + 4 - 4 t + 4 - 4 t ) d t

= ([(2)/(3) t^3]|_0^1 + ([(2)/(3) t^3 + 8 t - (8)/(2) t^2]|_1^2

= (2)/(3) (8 - 1 + 1) + 8 (2 - 1) - 4 (4 - 1)

= (16)/(3) + 8 - 12

= (4)/(3)

Terminamos por aqui. Pode comemorar! \o/

Te vejo na próxima resolução

: )

Resposta

int_C F * d vec r = (4)/(3)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja F → um campo vetorial contínuo em R 2 . Justifique as igualdades. ∫ γ 1 F → ⋅ d γ → 1 = - ∫ γ 2 F → ⋅ d γ → 2 Onde γ 1 t = t , t 3 , - 1 ≤ t ≤ 1 , e γ 2 u = 1 - u , ( 1 - u 3 ,0 ≤ u ≤ 2
Seja F → um campo vetorial contínuo em R 2 . Justifique as igualdades. ∫ γ 1 F → ⋅ d γ → 1 = - ∫ γ 2 F → ⋅ d γ → 2 Onde γ 1 t = cos ⁡ t , s e nt , 0 ≤ t ≤ 2 π , e γ 2 u = cos ⁡ ( 2 π - u ) , s e n2 π
Seja F → um campo vetorial contínuo em R 2 . Justifique as igualdades. ∫ γ 1 F → ⋅ d γ → 1 = ∫ γ 2 F → ⋅ d γ → 2 Onde γ 1 t = t , t 2 , 0 ≤ t ≤ 1 , e γ 2 u = u 2 , u 2 2 ,0 ≤ u ≤ 2
Seja F → um campo vetorial contínuo em R 2 . Justifique as igualdades. ∫ γ 1 F → ⋅ d γ → 1 = ∫ γ 2 F → ⋅ d γ → 2 Onde γ 1 t = cos ⁡ t , s e nt , 0 ≤ t ≤ 2 π , e γ 2 u = cos ⁡ 2 u , s e n2 u ,0 ≤ u ≤ π
Seja F → um campo vetorial contínuo em Ω e sejam γ 1 : a , b → Ω e γ 2 : c , d → Ω duas curvas quaisquer de classe C 1 , tais que I mγ 1 = I mγ 2 . A afirmação ∫ γ 1 F → ⋅ d γ 1 = ∫ γ 2 F → ⋅ d γ 2 Ou