Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 2.4 - Ex. 2
Use o gráfico dado de para encontrar um número tal que
se então
Passo 1
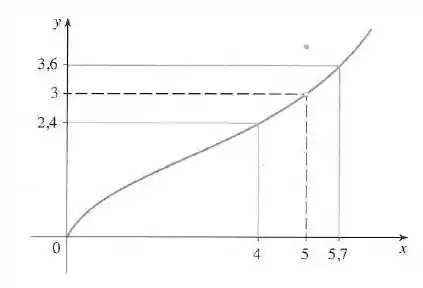
Opa, bora lá! Aqui temos o seguinte gráfico:
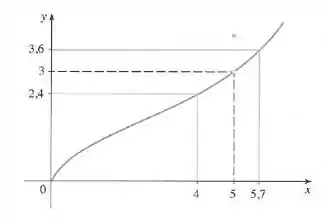
Estamos interessados na região próxima do ponto . Podemos reescrever a desigualdade
como
Assim, precisamos determinar os valores de para os quias a curva está entre as restas horizontais e .
Passo 2
Agora,olhando no gráfico as três funções próximo do ponto , e vemos o ponto de intersecção da curva com as restas é:
Vemos que esse intervalo não é simétrico em torno de , a distância até a extremidade esquerda é , e a distância até a extremidade direita é .
Podemos escolher como o menor desses números, isto é . Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.
Resposta
Exercícios de Livros Relacionados
Use o gráfico dado de f x = x para encontrar um número δ tal quese x - 4δ então x - 20,4
Use o gráfico dado de f x = x ² ² para encontrar um número δ tal quese x - 1δ então x ² - 11 2 ²
(a) Encontre um número δ tal que se x - 2δ , então 4 x - 8ε , onde ε = 0,1 .(b) Repita a parte (a) com ε = 0,01 .
Use o gráfico para encontrar um número N tal que, se xN , então 3 x 2 + 1 2 x 2 + x + 1 - 1,50,05
Resolva as inequações. x3