Use o gráfico para encontrar um número tal que, se , então:
Passo 1
E aíi, tudo bem?
Nesse problema a gente tem que usar um gráfico pra encontrar um número , onde , tal que:
Hãaam??!!
Esse é um número que se encontra na coordenada do eixo do gráfico que a gente vai fazer!
Esse exercício tem aquele sinalizinho rosa do lado no livro. Isso significa que ele leva em conta que você tem alguma ferramenta gráfica em mãos! Então não precisamos nos preocupar em desenhar esse gráfico esquisito na mão!
Vamos dizer que:
Aqui a gente precisa desenhar o gráfico de , não esquece de colocar o módulo! Então a gente vai traçar uma reta no eixo em e ver onde essa reta cruza a curva e anotamos a coordenada correspondente.
Lembra que devemos ter:
E:
Com o gráfico em mãos a gente escolhe um no eixo que atende esses dois critérios! Bora lá?!
Passo 2
Vamos desenhar o gráfico da função:
E a reta:
Assim:
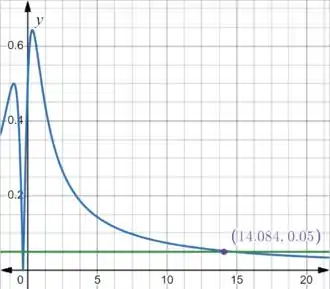
As curvas se tocam em , então queremos um ponto onde xe.
Podemos escolher qualquer , então aqui vamos escolher:
Prontinho!