Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 2.4 - Ex. 6
Use um gráfico para encontrar um número tal que
se então
Passo 1
Fala aí, tudo certinho com você?
Bom, essa questão pede pra gente usar um gráfico para encontrar um número tal que sempre que .
O que devemos fazer aqui é dizer qual é o número que respeita essa condição. Vamos então traçar o gráfico de para ver isso acontecendo. Vem que te ajudo com isso.
Passo 2
Antes de plotarmos o gráfico vamos fazer algumas modificações na expressão para tornar nossa resolução mais simples. Observe que:
Tirando do módulo, teremos:
E resolvendo dos dois lados, ficamos com:
Perfeito!
Assim, precisamos determinar os valores de para os quais a curva está entre as restas horizontais e .
Passo 3
Agora, vamos plotar o gráfico das três funções:
E obtemos o seguinte gráfico:
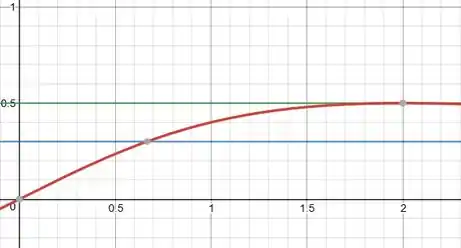
Passo 4
Vemos o ponto de intersecção da curva com as retas nos dá:
Vemos que esse intervalo não é simétrico em torno de .
Dessa forma, podemos verificar um valor para
Nosso vai ser o valor mínimo entre os 2, portanto,
Podemos escolher como o menor desses números para não sairmos do intervalo desejado, isto é . Embora tenhamos escolhido , qualquer valor menor positivo de também funcionaria.