Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.3 - Ex. 34
Use um gráfico para estimar as coordenadas de dos pontos de interseção das curvas dadas. Então use essa informação para estimar o volume do solido obtido pela rotação ao redor do eixo da região limitada por essas curvas.
,
Passo 1
Pra começar vamos fazer um gráfico para achar os pontos de interseção entre , . Olha só:
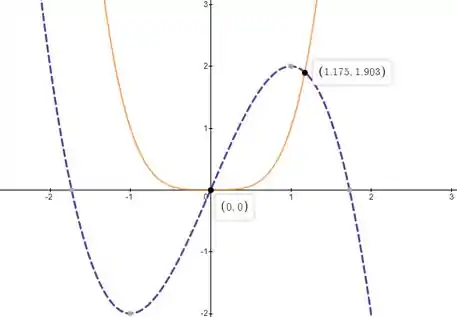
A ideia vai ser achar o volume gerado pela rotação da curva não pontilhada e subtrair volume gerado pela rotação da curva pontilhada. Usando o método das cascas, vamos integrar entre os ponto e .
Assim,
Não esquece:quando
Passo 2
Integrando, temos:
Aplicando entre esses pontos:
Jogando na maquinha:
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 A
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 D
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 E
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 E
Nos Exercícios 23-26, use o método da casca para determinar o volume dos sólidos obtidos com a rotação das regiões delimitadas pelas curvas dadas em torno das retas dadas.23 - y = 3 x ,y = 0 ,y = 2 B