Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 6.3 - Ex. 42
A região limitada pelas curvas dadas é girada ao redor dos eixos especificados. Ache o volume do solido resultante por qualquer método.
; ao redor do eixo
Passo 1
A equação que ele nos deu foi a seguinte:
Mas lá da trigonometria a gente sabe que isso representa uma circunferência com centro em e raio igual a . Fazendo um gráfico, temos:
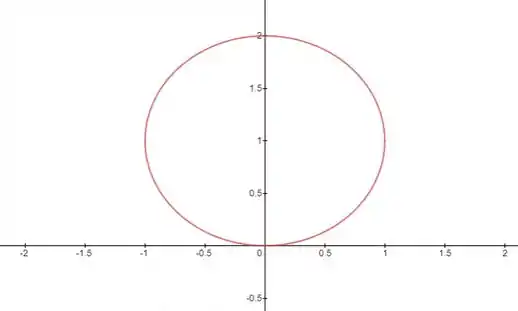
Opa, mas o volume da circunferência é conhecido. Deixa eu te lembrar:
Como :
Resposta
Exercícios de Livros Relacionados
Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir. y = x ,y = - x 2 ,x = 2
Nos Exercícios 1-6, use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
Nos Exercícios 1-6, use o método da casca para determinar os volumes dos sólidos obtidos com a rotação das regiões sombreadas em torno dos eixos indicados.
Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir. y = 2 x ,y = x 2 ,x = 1
Nos Exercícios 7-12, use o método da casca para determinar o volume do sólido obtido com a rotação em torno do eixo y das regiões limitadas pelas curvas e retas a seguir. y = x 2 ,y = 2 - x ,x = 0 , p