Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 2.2 - Ex. 53
Use um gráfico para obter estimativas das equações de todas as assíntotas verticais da curva:
A seguir, encontre as equações exatas dessas assíntotas.
Passo 1
Eaee, belezinha?? Bom... o enunciado nos deu a seguinte função:
Para o intervalo .
Queremos plotar o gráfico dessa curva nesse intervalo e estimar as equações das assíntotas verticais.
Mas o que são essas assíntotas verticais???
Bom... As assíntotas verticais são linhas verticais nas quais uma função se aproxima à medida que a variável independente se aproxima de um determinado valor.
Elas são caracterizadas por valores extremos nos quais a função tende a infinito positivo ou negativo.
Assim, basta analisar no gráfico onde a função tende ao infinito em .
Em seguida, deveremos calcular a equação dessas assíntotas e comparar com o que encontramos das estimativas que fizemos.
Agora bora lá!! 😉
Passo 2
Começaremos o exercício plotando o gráfico da função fornecida no enunciado no intervalo especificado:
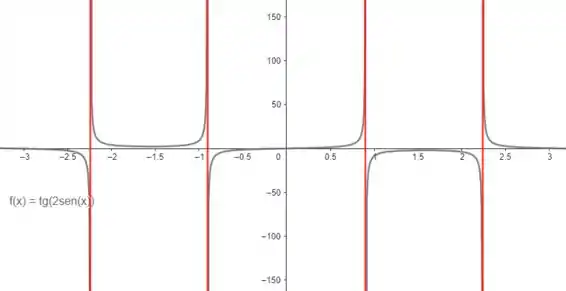
É possível notar que temos assíntotas (marcadas em vermelho) para e .
Passo 3
Para achar as equações exatas das assíntotas, devemos notar que o gráfico da tangente tem assíntotas verticais para:
Sendo assim, devemos ter:
Passo 4
Do círculo trigonométrico, sabemos que:
Com isso e a última relação obtida no passo 3, temos:
Esse valor corresponde a . E o seu ângulo complementar:
Corresponde a assíntota em .