Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.4 - Ex. 45
Use um gráfico para estimar a intersecção com o eixo da curva . A seguir, use essa informação para estimar a área da região que se situa sob a curva e acima do eixo .
Passo 1
Fala aí! tudo certinho?
Nesse problema temos que plotar o gráfico de
E estimar as intersecções com o eixo para assim calcular a área da curva acima do eixo .
Tem ideia de como fazemos isso?
Primeiro vamos usar uma ferramenta gráfica para estimar os valores de onde e para calcular a área de acima do eixo temos que lembrar que a integral de uma curva em um intervalo pode ser interpretado como a área abaixo da curva nesse intervalo.
Sacou? Bora começar!
Passo 2
Primeiro vamos estimar a intersesção com o eixo da curva , para isso vamos plotar o gráfico:
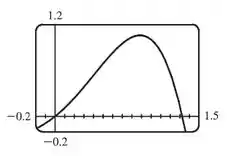
Pelo gráfico dá pra perceber que a interseção com o eixo é em e em mais ou menos .
Show?
Passo 3
Agora vamos estimar a área da região que se situa sob a curva e acima do eixo , para fazer isso devemos calcular a integral da curva de cima menos a de baixo, e usar os limites de integração com os pontos de intersecção que acabamos de achar.
A curva de cima é , a de baixo é o eixo , que seria , vamos agora montar a integral:
Onde e , que são os valores que estimamos no passo anterior.
Para calcular a integral dessa função, podemos usar a regra da potência já que a função de integração é um polinômio:
Aplicando essa regra na nossa integral:
Aplicando os limites de integração...
Portanto, a área abaixo da curva e acima do eixo é dada por:
E aí! o que achou? Responde Aí!
Resposta
Intersecção em e