Determine a área da região” triangular” no primeiro quadrante , limitada à esquerda pelo eixo e à direita pelas curva e

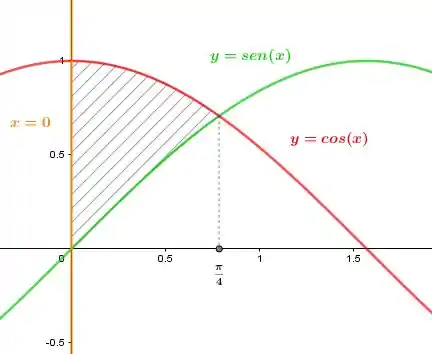Esboçando o gráfico da função, seja por um software, ou substituindo alguns valores em cada umas das funções para obter pontos, teremos um gráfico como esse ou parecido,

Onde, pelo que podemos é a função que está por cima , é a função que está por baixo e a parte hachurada é região que desejamos .Sendo assim a integral será :

Cujos limites de integração foram obtidos, a partir de onde a parte hachurada começa até o ponto de intersecção entre as duas curvas.

Já que encontramos a “cara” integral que para determinar a área, então vamos partir para os cálculos e ver quando essa integral vai dar, ou seja,

Usando a regra da subtração (a integral da subtração é a subtração das integrais)

=

Usando o Teorema Fundamental do Cálculo Parte II,

Portanto,