Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 4.3 - Ex. 55
(a) Use um gráfico de para estimar os valores máximo e mínimo. Então, encontre os valores exatos.
(b) Estime o valor de em que cresce mais rapidamente. Então, encontre o valor exato.
Passo 1
Oiii galerinha, vamos resolver essa juntinhos?
Nos precisamos utilizar um gráfico, correto?Possuimos diversas ferramentas para plotar o mesmo, porém, vamos utilizar a ferramenta mais comum, que e o nosso geogebra, para plotar esse gráfico.
Podemos observar o comportamento da função e estimar os valores máximos e mínimos.
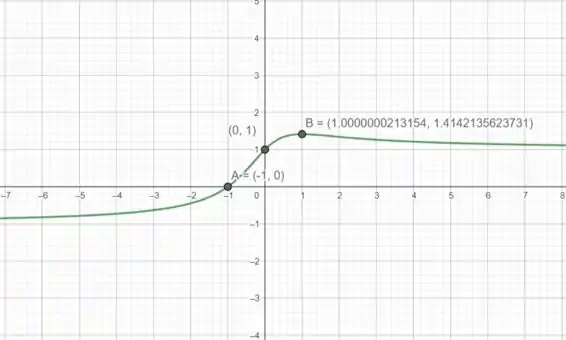
Agora bora resolver essa questão na raça, rsrs or no!
Vamos lá ...
Passo 2
Letra (a): Valores máximo e mínimo
Para encontrar os valores exatos, precisamos encontrar os pontos críticos de Isso é feito derivando a função e igualando a derivada a zero.
A função dada é
Derivamos usando a regra do quociente e a regra da cadeia:
Primeiro, calculamos
Agora, substituímos na fórmula do quociente:
Passo 3
Simplificamos a derivada:
Para encontrar os pontos críticos, igualamos a derivada a zero:
Passo 4
Agora, avaliamos nos pontos críticos e nos limites do domínio da função.
Verificamos
Como é contínua e definida para todos os reais, verificamos os limites quando .
Portanto, os valores máximo e mínimo são , respectivamente.
Passo 5
Letra (b): Estimar o valor de em que cresce mais rapidamente
O crescimento mais rápido da função geralmente ocorre onde a derivada é máxima.
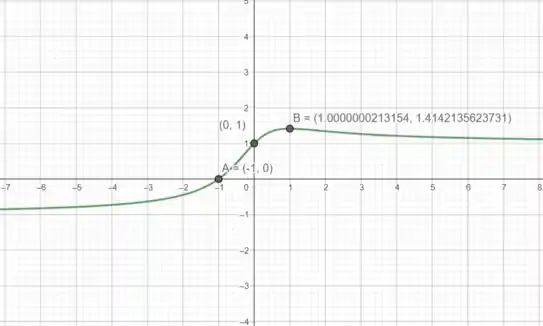
Para encontrar o ponto onde a função cresce mais rapidamente, procuramos o máximo de . Analisamos a derivada segunda de
Derivamos novamente para encontrar
Passo 6
Usamos a regra do quociente novamente. Sem a expressão detalhada, podemos ver que para a primeira derivada, o crescimento é mais rápido onde a derivada é máxima. A análise da derivada segunda nos dá informações sobre a concavidade e pontos de inflexão. Resolvendo , encontramos onde muda de concavidade.
Analisando a função e suas derivadas, o crescimento mais rápido (máximo de ocorre próximo de
Verificamos se este ponto é um máximo local da derivada:
Avaliamos
Analisando o comportamento de perto de determinamos que é um ponto onde a função cresce mais rapidamente.
Resposta
(a) Ponto de máximo local é .(b) cresce mais rápido em .