Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.3 - Ex. 60
- Use um gráfico de para estimar os valores máximo e mínimos. Então, encontre os valores exatos.
- Estime o valor de em que cresce mais rapidamente. Então, encontre o valor exato.
Passo 1
Essa questão vamos precisar de um software. O que vamos utilizar aqui é o geogebra, beleza?
Inicialmente ela quer que esbocemos o gráfico da função dada:
Para estimarmos os valores máximos e mínimos.Então vamos encontrar os valores exatos, e para isso vamos derivar a função e igualar a zero.depois, vamos com o gráfico estimar onde a função cresce mais rapidamente e então a partir da derivada encontrar esse valor (ele será onde a derivada tiver o maior valor, afinal a derivada indica o quanto a função cresce.
Passo 2
Vamos esboçar o gráfico no software.
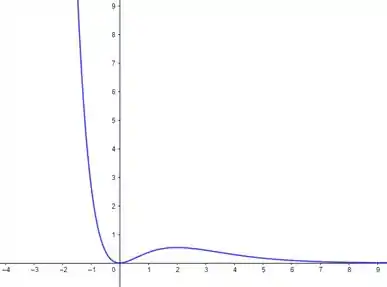
Vamos resolver o item a)
Olhando para o gráfico, podemos notar que a função tem 1 máximo local e 1 mínimo local.
O máximo ocorre ali no ponto e o mínimo local ocorre em .
Passo 3
Agora vamos usar o cálculo para encontrar esses pontos.Para isso eu preciso derivar a minha função, que é:
Para derivar vamos usar a regra do produto, pois temos uma multiplicação de funções e a regra da cadeia para a função :
Igualando a zero temos:
Fatorando, temos:
O termo nunca zera, portanto temos que:
Fatorando temos:
Dessa forma, os pontos críticos e portanto candidatos a máximos e mínimos locais são:
E
Conforme vimos no gráfico da função.
Passo 4
Para a gente tentar estimar onde a função cresce mais rapidamente, ou seja, precisamos analisar o gráfico de e encontrar o máximo.
Esboçando o gráfico,
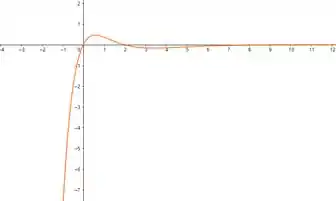
Marcando os pontos de máximo e mínimo,
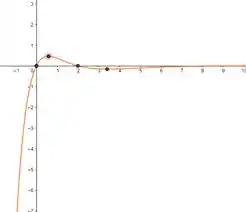
Temos que o máximo de .
Logo, é o valor que cresce mais rapidamente.
Agora usando o cálculo, podemos derivar a derivada e então igualar a segunda derivada a zero.
Derivando novamente temos:
Portanto,
Igualando a zero, apenas o polinômio de segundo grau pode zerar:
Resolvendo por Bhaskara temos:
Vemos pelo gráfico que o ponto de máximo é o ponto
Resposta
O ponto é o máximo local e o ponto é o mínimo local. A função cresce mais rápido em